
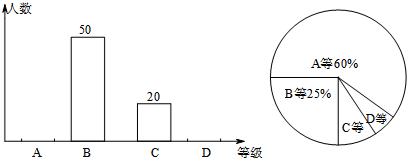
| A. | 样本容量是200 | |
| B. | 样本中C等所占百分比是10% | |
| C. | D等所在扇形的圆心角为15° | |
| D. | 估计全校学生成绩为A等大约有900人 |
分析 根据条形统计图和扇形统计图提供的数据分别列式计算,再对每一项进行分析即可.
解答 解:A、$\frac{50}{25%}$=200(名),则样本容量是200,故A不符合题意;
B、样本中C等所占百分比是1-60%-25%-$\frac{10}{200}$×100%=10%,故B不符合题意;
C、成绩为A的人数是:200×60%=120(人),
成绩为D的人数是200-120-50-20=10(人),
D等所在扇形的圆心角为:360°×$\frac{10}{200}$=18°,故C符合题意;
D、全校学生成绩为A等大约有1500×60%=900人,故D不符合题意.
故选:C.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
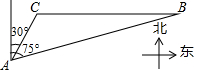 如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C 100米的地方选择了一个固定观测点A,并测得小岛C在观侧点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321)
如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C 100米的地方选择了一个固定观测点A,并测得小岛C在观侧点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知点A(-2,-4),直线x=-2与x轴相交于点B,连接OA,抛物线y=-x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到点A时停止移动.
如图,在平面直角坐标系中,已知点A(-2,-4),直线x=-2与x轴相交于点B,连接OA,抛物线y=-x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到点A时停止移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com