
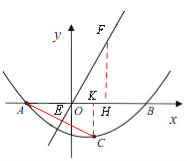
【题目】如图①,若二次函数![]() 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数![]() 的图象的对称点为C。
的图象的对称点为C。
(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
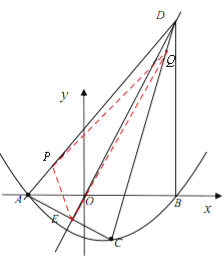
(3)如图②,过点B作DB⊥x轴交正比例函数![]() 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数![]() 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。

【答案】(1)![]() 。
。
(2)利用轴对称和锐角三角函数求出点C的坐标,代入![]() 验证即可。
验证即可。
(3)存在时刻![]() ,使PE平分∠APQ,同时QE平分∠PQC。
,使PE平分∠APQ,同时QE平分∠PQC。
【解析】
分析:(1)将A(-2,0),B(3,0)两点坐标 代入![]() ,即可求出b、c的值。
,即可求出b、c的值。
(2)利用轴对称和锐角三角函数求出点C的坐标,代入![]() 验证即可。
验证即可。
(3)通过证明△PAE∽△ECQ,求出时间t。
解:(1)∵二次函数![]() 的图象与x轴交于点A(-2,0),B(3,0)两点,
的图象与x轴交于点A(-2,0),B(3,0)两点,
∴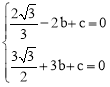 ,解得
,解得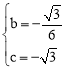 。
。
∴![]() 。
。
(2)证明:由(1)得二次函数解析式为![]() 。
。
在正比例函数![]() 的图象上取一点F
的图象上取一点F![]() ,作FH⊥x轴于点H,则
,作FH⊥x轴于点H,则
![]() 。∴
。∴![]() 。
。
连接AC交 ![]() 的图象于点E,作CK 垂直x轴于点K,
的图象于点E,作CK 垂直x轴于点K,
∵点A关于![]() 的图象的对称点为C,
的图象的对称点为C,
∴OE垂直平分AC。
∵![]() ,OA=2,
,OA=2,
∴![]() 。
。
在Rt△ACK中,∵![]() ,
,
∴![]() 。∴
。∴![]() 。
。
∴点C 的坐标为![]() 。
。
将C ![]() 代入
代入![]() ,左边=右边,
,左边=右边,
∴点C在所求的二次函数的图象上。
(3)∵DB⊥x轴交![]() 的图象于点D,B(3,0),
的图象于点D,B(3,0),
∴把x=3代入![]() 得
得![]() ,即BD=
,即BD=![]() 。
。
在Rt△ACK中,![]() ,
,
∵OE垂直平分AC,
∴![]() ,
,![]() 。
。
假设存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,
则![]() 。
。
∵![]() , ∴
, ∴![]() 。
。
又∵![]() ,∴
,∴![]() 。
。
又∵![]() ,∴△PAE∽△ECQ。∴
,∴△PAE∽△ECQ。∴![]() ,即
,即![]() 。
。
整理,得![]() ,解得
,解得![]() (不合题意,舍去)。
(不合题意,舍去)。
∴存在时刻![]() ,使PE平分∠APQ,同时QE平分∠PQC。
,使PE平分∠APQ,同时QE平分∠PQC。


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计(满分100分,学生成绩取整数),并按照成绩从低到高分成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个小组,绘制统计图如下(未完成),解答下列问题:
五个小组,绘制统计图如下(未完成),解答下列问题:

(1)样本容量为______,频数分布直方图中![]() ______;
______;
(2)扇形统计图中![]() 小组所对应的扇形圆心角为______度,并补全频数分布直方图;
小组所对应的扇形圆心角为______度,并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2![]() ,则MN的长为( )
,则MN的长为( )

A.2![]() B.4
B.4![]() C.5 D.6
C.5 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“校园献爱心”活动.准备向西部山区学校捐赠男、女两种款式的书包,已知男款书包单价![]() 元/个,女款书包单价
元/个,女款书包单价![]() 元/个.
元/个.
![]() 原计划募捐
原计划募捐![]() 元,恰好可购买两种款式的书包
元,恰好可购买两种款式的书包![]() 个,问两种款式的书包各买多少个?
个,问两种款式的书包各买多少个?
![]() 在捐款活动中,师生积极性高,实际捐款额和书包数量都高于原计划.快递公司将这些书包装箱运送,其中每箱书包数量相同.第一次他们领走这批的
在捐款活动中,师生积极性高,实际捐款额和书包数量都高于原计划.快递公司将这些书包装箱运送,其中每箱书包数量相同.第一次他们领走这批的![]() ,结果装了
,结果装了![]() 箱还多
箱还多![]() 个书包;第二次他们把余下的
个书包;第二次他们把余下的![]() 领走.连同第一次装箱剩下的
领走.连同第一次装箱剩下的![]() 个书包一起,刚好装了
个书包一起,刚好装了![]() 箱.问:实际购买书包共多少个?
箱.问:实际购买书包共多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )

A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B分别在x轴、y轴上,点O关于AB的对称点C在第一象限,将△ABC沿x轴正方向平移k个单位得到△DEF(点B与E是对应点),点F落在双曲线y=![]() 上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 ________ .
上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 ________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边BC在x轴上,点A(a,4)和D分别在反比函数y=-![]() 和y=
和y=![]() (m>0)的图象上.
(m>0)的图象上.

(1)当AB=BC时,求m的值。
(2)连结OA,OD.当OD平方∠AOC时,求△AOD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一分钟投篮测试规定,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:
成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
甲组(人) | 1 | 2 | 5 | 2 | 1 | 4 |
乙组(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(1)请你根据上述统计数据,把下面的图和表补充完整;

一分钟投篮成绩统计分析表:
统计量 | 平均分 | 方差 | 中位数 | 合格率 | 优秀率 |
甲组 | 2.56 | 6 | 80.0% | 26.7% | |
乙组 | 6.8 | 1.76 | 86.7% | 13.3% |
(2)下面是小明和小聪的一段对话,请你根据(1)中的表,写出两条支持小聪的观点的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
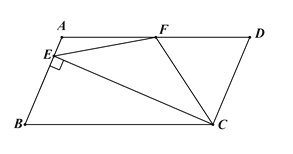
【题目】如图,在平行四边形 ABCD 中, AD 2 AB ;CF 平分 BCD 交 AD 于 F ,作 CE AB , 垂足 E 在边 AB 上,连接 EF .则下列结论:① F 是 AD 的中点; ② S△EBC 2S△CEF;③ EF CF ; ④ DFE 3AEF .其中一定成立的是_____.(把所有正确结论的序号都填在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com