
【题目】如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长. 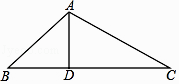
科目:初中数学 来源: 题型:
【题目】某市居民生活用水的费用由“城市供水费” 和“污水处理费” 两部分组成.为了鼓励市民节约用水,其中城市供水费按阶梯式计费:一个月用水10吨以内(包括10吨)的用户,每吨收1.5元;一个月用水超过10吨的用户,10吨水仍按每吨1.5元收费,超过10吨的部分,按每吨2元收费.另外污水处理费按每吨0.65元收取.
(1)某居民5月份用水8吨,应交水费多少元? 6月份用水12吨,应交水费多少元?
(2)若某户某月用水x吨,请你用含有x的代数式表示该月应交的水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个老太太提着一个篮子去卖鸡蛋,第一个人买走了她的鸡蛋的一半又半个;第二个人买走了剩下的一半又半个;第三人买走了前两个人剩下的一半又半个,正好卖完全部鸡蛋,问老太太一共卖了多少个鸡蛋.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点. (Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.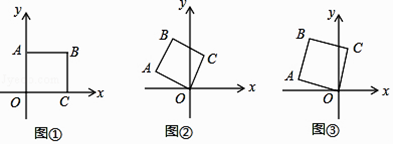
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在网格中建立平面直角坐标系,每个小正方形的边长都是1个单位长度,四边形ABCD的各顶点均在网格点上.
(1)将四边形ABCD平移,使得D点平移到D1(3,4),画出平移后的四边形A1B1C1D1;
(2)画出四边形ABCD绕着原点O逆时针旋转90°后的四边形A2B2C2D2.
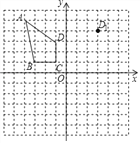
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王计划租一间商铺,下面是某房屋中介提供的两种商铺的出租信息:

设租期为x(月),所需租金为y(元),其中x为大于1的整数.
(1)若小王计划租用的商铺为90m2,请分别写出在商座A,B租商铺所需租金yA(元),yB(元)与租期x(月)之间的函数关系式;
(2)在(1)的前提下,请你帮助小王根据租期,租用哪个商座的商铺房租更低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内直角坐标系中,直线l:y= ![]() x+1交x轴于点A,交y轴于点B,点A1 , A2 , A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则OAn的长是( )
x+1交x轴于点A,交y轴于点B,点A1 , A2 , A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则OAn的长是( )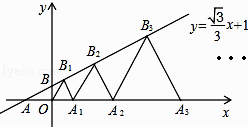
A.2n ![]()
B.(2n+1) ![]()
C.(2n﹣1﹣1) ![]()
D.(2n﹣1) ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线L:y=ax2+bx+c与已知抛物线y= ![]() x2的图像的形状相同,开口方向也相同,且顶点坐标为(﹣2,﹣4)
x2的图像的形状相同,开口方向也相同,且顶点坐标为(﹣2,﹣4)
(1)求L的解析式;
(2)若L与x轴的交点为A,B(A在B的左侧),与y轴的交点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图①中△ABC是等边三角形,其边长是3,图②中△DEF是等腰直角三角形,∠F=90°,DF=EF=3.
(1)若S1为△ABC的面积,S2为△DEF的面积,S3=![]() AB·BC·sinB,S4=
AB·BC·sinB,S4=![]() DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;
DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;
![]()
(2)在图③中,∠P=α(α为锐角),OP=m,PQ=n,△OPQ的面积为S,请你根据第(1)小题的解答,直接写出S与m,n以及α之间的关系式,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com