
| 转让数量(套) | 1200 | 1100 | 1000 | 900 | 800 | 700 | 600 | 500 | 400 | 300 | 200 | 100 |
| 价格(元/套) | 240 | 250 | 260 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 |
分析 (1)猜想转让价格与转让数量之间的函数关系为一次函数,设转让价格为x(元/套),转让数量y(套),则转让价格与转让数量之间的函数关系式为:y=kx+b,把两对对应值代入解方程组可得结果;
(2)根据利润=(售价-成本)×销售量,由方案1:不转让A品牌服装,也不经销B品牌服装,直接求解即可求得答案;由方案2:由全部转让A品牌服装,用转让得来的资金一次性购入B品牌服装后,经销B品牌服装,首先求得转让款,又分析可得可购进B品牌服装,一年内刚好卖完,根据利润的求解方法求得答案;由方案3:设转让A品牌服装x套,则转让价格是每套360-$\frac{x}{10}$元,可进购B品牌服装$\frac{\frac{x(360-x)}{10}}{200}$套,列出利润与x之间的函数关系式,求其最大值,即可求得答案.
解答 解:(1)猜想转让价格与转让数量之间的函数关系为一次函数,
设转让价格为x(元/套),转让数量y(套),
则转让价格与转让数量之间的函数关系式为:y=kx+b,
∴$\left\{\begin{array}{l}{600=300k+b}\\{100=350k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-10}\\{b=3600}\end{array}\right.$,
∴转让价格与转让数量之间的函数关系式为:y=-10x+3600;
(2)解:经销商甲的进货成本是1200×400=480000(元),
选方案1,则获利1200×600-480000=240000(元),
若选方案2,得转让款1200×240=288000(元),
可购进B品牌服装288000÷200=1440(套),
一年内刚好卖完,
可获利1440×500-480000=240000(元),
若选择方案3,设转让A品牌服装x套,则转让价是每套(360-$\frac{x}{10}$)元
可得转让资金x(360-$\frac{x}{10}$)元
那么可购进B品牌服装$\frac{\frac{x(360-x)}{10}}{200}$套,
全部售出B品牌服装后得款500×$\frac{\frac{x(360-x)}{10}}{200}$=$\frac{5}{2}$x(360-$\frac{x}{10}$),
此时,还剩A品牌服装(1200-x)套,
全部售出A品牌服装后得款600(1200-x)(元)
共获利:$\frac{5}{2}$x(360-$\frac{x}{10}$)+600(1200-x)-480000=-$\frac{1}{4}$(x-600)2+330000,
∴当x=600(套),可获最大利润330000元.
答:选择第三种方案在一年内获得利润最大,当他转让给经销商乙的A品牌服装的数量是600套时,可获最大利润330000元.
点评 本题主要考查二次函数的实际应用问题.此题难度较大,解题的关键是理解题意,根据利润=(售价-成本)×销售量,列出函数关系式,求出最值,注意灵活运用二次函数解决实际问题.


科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{\frac{1}{x}+y=4}\\{x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1=1}\\{y-z=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y=2x+5}\\{3x=-6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{xy=1}\\{x+y=2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
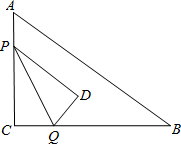 在Rt△ABC中,∠C=90°,AC=12,BC=16,动点P从点A出发沿AC边向点C以每秒3个单位长度的速度运动,动点Q从点C出发沿着CB边向点B以每秒4个单位长的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另一个点也随之停止运动.在运动过程中,△PCQ关于直线PQ对称的图形是△PDQ.设运动时间为t(秒),是否存在时刻t,使得PD∥AB?若存在,求出t的值;若不存在,请说明理由.
在Rt△ABC中,∠C=90°,AC=12,BC=16,动点P从点A出发沿AC边向点C以每秒3个单位长度的速度运动,动点Q从点C出发沿着CB边向点B以每秒4个单位长的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另一个点也随之停止运动.在运动过程中,△PCQ关于直线PQ对称的图形是△PDQ.设运动时间为t(秒),是否存在时刻t,使得PD∥AB?若存在,求出t的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=9cm,动点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为3.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=9cm,动点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 61 | B. | 63 | C. | 65 | D. | 62 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com