
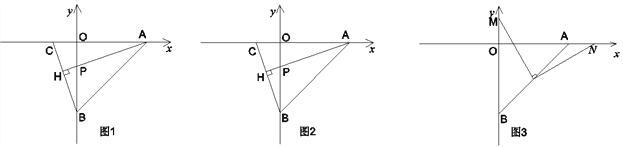
【题目】如图1,直线AB交x轴于点A(4 ,0),交y轴于点B(0 ,4),
(1)如图,若C的坐标为(-1, ,0),且AH⊥BC于点H,AH交OB于点P,试求点P的坐标;
(2)在(1)的条件下,如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连结MD,过点D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,式子![]() 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
【答案】(1)P(0 ,1);(2)证明见解析;(3)4.
【解析】试题分析:(1)利用坐标的特点,得出△OAP≌△OB,得出OP=OC=1,得出结论;
(2)过O分别做OM⊥CB于M点,ON⊥HA于N点,证出△COM≌△PON,得出OM=ON,HO平分∠CHA,求得结论;
(3)连接OD,则OD⊥AB,证得△ODM≌△ADN,利用三角形的面积进一步解决问题.
试题解析:(1)由题得,OA=OB=4.
∵AH⊥BC于H,
∴∠OAP+∠OPA=∠BPH+∠OBC=90°,
∴∠OAP=∠OBC
在△OAP和△OBC中,
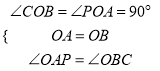
∴△OAP≌△OBC(ASA),
∴OP=OC=1,则点P(0 ,1).
(2)过点O分别作OM⊥CB于M点,ON⊥HA于N点,
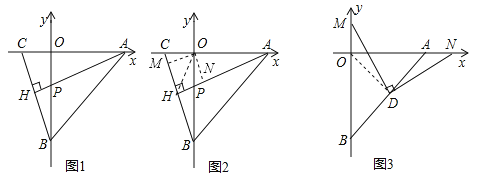
在四边形OMHN中 ,∠MON=360°-3×90°=90°,
∴∠COM=∠PON=90°-∠MOP.
在△COM和△PON中,
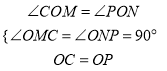 ,
,
∴△COM≌△PON(AAS),
∴OM=ON,
∵HO平分∠CHA,
∴![]() ;
;
(3) ![]() 的值不发生改变,
的值不发生改变, ![]() .
.
理由如下:
连结OD,则OD⊥AB,∠BOD=∠AOD=45°,∠OAD=45°,
∴OD=AD,
∴∠MDO=∠NDA=90°-∠MDA,
在△ODM和△AND中,
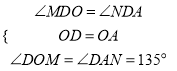 ,
,
∴△ODM≌△AND(ASA),
∴![]()
∴![]() ,
,
∴![]()


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米.

查看答案和解析>>
科目:初中数学 来源: 题型:
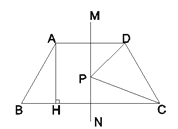
【题目】如图,题型ABCD中,AD∥BC,AD=CD=AD=2,∠B=60°,AH⊥BC于点H,且AH=![]() ,直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为______.
,直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
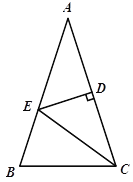
【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=12,求BC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上 ,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上 ,称为二次变换,……经过连续2017次变换后,顶点A的坐标是:

A. (4033, ![]() ) B. (4033,0) C. (4036,
) B. (4033,0) C. (4036, ![]() ) D. (4036,0)
) D. (4036,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块长18米,宽15米的矩形荒地修建成一个花园(阴影部分)所占的面积为原来荒地面积的三分之二.(精确到0.1m)
(1)设计方案1(如图1)花园中修两条互相垂直且宽度相等的小路.
(2)设计方案2(如图2)花园中每个角的扇形都相同.
以上两种方案是否都能符合条件?若能,请计算出图1中的小路的宽和图2中扇形的半径;若不能符合条件,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°.
(1) 求∠DAC的度数.
(2) 求证:△ACD是等腰三角形.
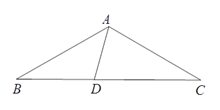
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com