
| A. | 42 | B. | 32 | C. | 42或32 | D. | 42或37 |
分析 本题应分两种情况进行讨论:
(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;
(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
解答 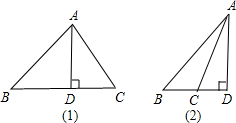 解:此题应分两种情况说明:
解:此题应分两种情况说明:
(1)当△ABC为锐角三角形时,在Rt△ABD中,
BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=9,
在Rt△ACD中,
CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=5
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;
(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD=9,
在Rt△ACD中,CD=5,
∴BC=9-5=4.
∴△ABC的周长为:15+13+4=32
∴当△ABC为锐角三角形时,△ABC的周长为42;当△ABC为钝角三角形时,△ABC的周长为32.
综上所述,△ABC的周长是42或32.
故选:C.
点评 此题考查了勾股定理及解直角三角形的知识,在解本题时应分两种情况进行讨论,易错点在于漏解,同学们思考问题一定要全面,有一定难度.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
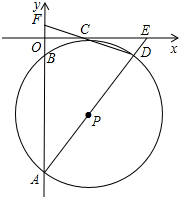 如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为(0,2),点D的坐标为(6,-2).
如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为(0,2),点D的坐标为(6,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2条 | B. | 3条 | C. | 5条 | D. | 6条 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
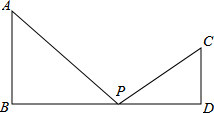 如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.
如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}{x^2}+2x+1=0$ | B. | 0.1x2-0.5x+1.8=0 | ||
| C. | $\frac{1}{2}{x^2}=1-\frac{3}{5}x$ | D. | x2+x-1=(x+1)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com