
分析 (1)由△PBC∽△PAM,推出∠PAM=∠PBC,由∠PBC+∠PBA=90°,推出∠PAM+∠PBA=90°即可证明AP⊥BN,由△PBC∽△PAM,推出$\frac{PM}{PC}$=$\frac{AM}{BC}$=$\frac{PA}{PB}$,由△BAP∽△BNA,推出$\frac{PA}{PB}$=$\frac{AN}{BC}$,得到$\frac{AN}{AB}$=$\frac{AM}{BC}$,由此即可证明.
(2)①结论仍然成立,证明方法类似(1).②这样的点P不存在.利用反证法证明.假设PC=$\frac{1}{2}$,推出矛盾即可.
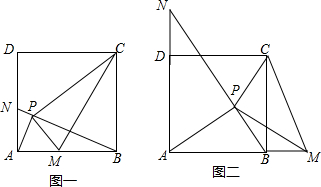
解答 (1)证明:如图一中,∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,
∵△PBC∽△PAM,
∴∠PAM=∠PBC,$\frac{PM}{PC}$=$\frac{AM}{BC}$=$\frac{PA}{PB}$,
∴∠PBC+∠PBA=90°,
∴∠PAM+∠PBA=90°,
∴∠APB=90°,
∴AP⊥BN,
∵∠ABP=∠ABN,∠APB=∠BAN=90°,
∴△BAP∽△BNA,
∴$\frac{PA}{PB}$=$\frac{AN}{BC}$,
∴$\frac{AN}{AB}$=$\frac{AM}{BC}$,
∵AB=BC,
∴AN=AM.
(2)解:①仍然成立,AP⊥BN和AM=AN.
理由如图二中,∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,
∵△PBC∽△PAM,
∴∠PAM=∠PBC,$\frac{PM}{PC}$=$\frac{AM}{BC}$=$\frac{PA}{PB}$,
∴∠PBC+∠PBA=90°,
∴∠PAM+∠PBA=90°,
∴∠APB=90°,
∴AP⊥BN,
∵∠ABP=∠ABN,∠APB=∠BAN=90°,
∴△BAP∽△BNA,
∴$\frac{PA}{PB}$=$\frac{AN}{AB}$,
∴$\frac{AN}{AB}$=$\frac{AM}{BC}$,
∵AB=BC,
∴AN=AM.
②这样的点P不存在.
理由:假设PC=$\frac{1}{2}$,
如图三中,以点C为圆心$\frac{1}{2}$为半径画圆,以AB为直径画圆,
CO=$\sqrt{B{C}^{2}+B{O}^{2}}$=$\frac{\sqrt{5}}{2}$>$\frac{1}{2}$+$\frac{1}{2}$,
∴两个圆外离,∴∠APB<90°,这与AP⊥PB矛盾,
∴假设不可能成立,
∴满足PC=$\frac{1}{2}$的点P不存在.
点评 本题考查相似三角形综合题、正方形的性质、圆的有关知识,解题的关键是熟练应用相似三角形性质解决问题,最后一个问题利用圆的位置关系解决问题,有一定难度,属于中考压轴题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
 如图所示,小明在绣湖公园的A处正面观测解百购物中心墙面上的电子屏幕,测得屏幕上端C处的仰角为30°,接着他正对电子屏幕方向前进7m到达B处,又测得该屏幕上端C处的仰角为45°.已知电子屏幕的下端离开地面距离DE为4m,小杨的眼睛离地面1.60m,电子屏幕的上端与墙体的顶端平齐.求电子屏幕上端与下端之间的距离CD(结果保留根号).
如图所示,小明在绣湖公园的A处正面观测解百购物中心墙面上的电子屏幕,测得屏幕上端C处的仰角为30°,接着他正对电子屏幕方向前进7m到达B处,又测得该屏幕上端C处的仰角为45°.已知电子屏幕的下端离开地面距离DE为4m,小杨的眼睛离地面1.60m,电子屏幕的上端与墙体的顶端平齐.求电子屏幕上端与下端之间的距离CD(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 实数a,n,m,b满足a<n<m<b,这四个数在数轴上对应的点分别为A,N,M,B(如图),若AM2=BM•AB,BN2=AN•AB,则称m为a,b的“大黄金数”,n为a,b的“小黄金数”,当b-a=2时,a,b的大黄金数与小黄金数之差m-n=2$\sqrt{5}$-4.
实数a,n,m,b满足a<n<m<b,这四个数在数轴上对应的点分别为A,N,M,B(如图),若AM2=BM•AB,BN2=AN•AB,则称m为a,b的“大黄金数”,n为a,b的“小黄金数”,当b-a=2时,a,b的大黄金数与小黄金数之差m-n=2$\sqrt{5}$-4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
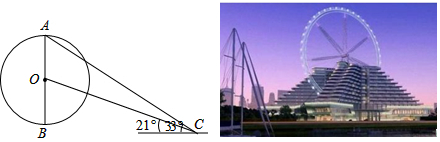
| A. | 169米 | B. | 204米 | C. | 240米 | D. | 407米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
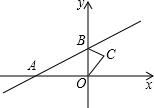 如图,直线y=$\frac{1}{2}$x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-8,-3)或(4,3).
如图,直线y=$\frac{1}{2}$x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-8,-3)或(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当x>0时,y随x的增大而增大 | B. | 当x=2时,y有最大值-3 | ||
| C. | 图象的顶点坐标为(-2,-7) | D. | 图象与x轴有两个交点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com