
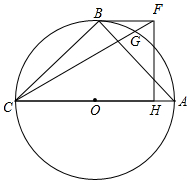
 如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.
如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.分析 (1)连接OG,利用弧长公式直接计算即可;
(2)结论:BF是⊙O的切线.连接OB,只要证明OB⊥BF即可;
解答 解:(1)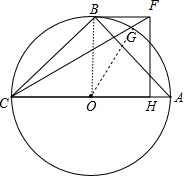 连接OG.
连接OG.
∵∠AOG=2∠ACF=60°,OA=4,
∴$\widehat{AG}$的长=$\frac{60•π•4}{180}$=$\frac{4}{3}$π.
(2)结论:BF是⊙O的切线.
理由:连接OB.
∵AC是直径,
∴∠CBA=90°,
∵BC=BA,OC=OA,
∴OB⊥AC,
∵FH⊥AC,
∴OB∥FH,
在Rt△CFH中,∵∠FCH=30°,
∴FH=$\frac{1}{2}$CF,
∵CA=CF,
∴FH=$\frac{1}{2}$AC=OC=OA=OB,
∴四边形BOHF是平行四边形,
∵∠FHO=90°,
∴四边形BOHF是矩形,
∴∠OBF=90°,
∴OB⊥BF,
∴BF是⊙O的切线.
点评 本题考查切线的判定、矩形的判定.等腰三角形的性质,直角三角形30度角的性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造特殊四边形解决问题.


科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平行四边形ABCO中,AO=1,AB=3,点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴上,若点D在反比例函数y=$\frac{k}{x}$的图象上,则k的值为$\sqrt{3}$.
如图,平行四边形ABCO中,AO=1,AB=3,点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴上,若点D在反比例函数y=$\frac{k}{x}$的图象上,则k的值为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2-2ab+b2=(a-b)2 | B. | xy+xz+x=x(y+z) | C. | x2+x3=x3($\frac{1}{x}$+1) | D. | a2+b2=(a+b)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
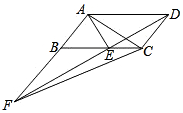 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CEF;⑤S△ABE=S△CDE.其中正确的是( )
如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CEF;⑤S△ABE=S△CDE.其中正确的是( )| A. | ①②③ | B. | ①②⑤ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在正方形ABCO中,A(0,4),B(4,4),C(4,0),O(0,0),E为AO的中点,F为边CO上的动点,分别连接EF,FB,BE得到△EFB,并将其沿FB折叠得到△E′FB.
在正方形ABCO中,A(0,4),B(4,4),C(4,0),O(0,0),E为AO的中点,F为边CO上的动点,分别连接EF,FB,BE得到△EFB,并将其沿FB折叠得到△E′FB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com