
如图所示,BF是半圆O的直径,△ABC内接于圆,过A点作AE⊥BF于E交BC于D.求证: =BD·BC.
=BD·BC.

|
证法一:连接 AF.
∵∠BAF=90°,∵AE⊥BF,∴∠BAE=∠F.∵∠C=∠F. ∴∠BAD=∠C.∵∠ABD是公用角,∴△BAD∽△BCA. ∴AB∶BD=BC∶AB.∴ 证法二:连接AF、CF.
∵BF是直径,∴∠BAF=90°,∠BCF=90°. ∵AE⊥BF,∴∠BED=90°.∵∠DBE公用,∴△BDE∽△BFC.∴BD·BF=BE·BF. ∵∠BAF=90°,∠AEB=90°,∴ ∴ |
|
所证的结论中, AB是△ABC的一边,而BD是因为AE⊥BF与BC相交得到的.这时若能证明△BAD△BCA,则结论就成立.从图中可观察到∠ABD是公共角,故需要证明∠BAD=∠C或∠BDA=∠BAC即可.这其中∠C是圆周角,而∠BAD不是,若能把它化为圆周角,则可证明结论成立.因∠BAD是直角三角形,所以需要找一个既在直角三角形中又是圆周角的角,考虑到BF是直径,若连接AF,则我们考虑的两点都可以实现. |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
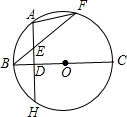 A是弧BF的中点,AH⊥BC.
A是弧BF的中点,AH⊥BC.查看答案和解析>>
科目:初中数学 来源: 题型:
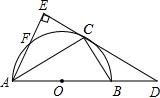 如图所示,已知AB是半圆O的直径,D是AB延长线上的一点,AE⊥DC,交DC的延长线于点E,交半圆O于点F,且C为
如图所示,已知AB是半圆O的直径,D是AB延长线上的一点,AE⊥DC,交DC的延长线于点E,交半圆O于点F,且C为 | BF |
查看答案和解析>>
科目:初中数学 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:047
| |||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com