
有一根长40mm的金属棒,欲将其截成x根7mm长的小段和y根9mm长的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A.x=1,y=3 B.x=3,y=2
C.x=4,y=1 D.x=2,y=3
科目:初中数学 来源: 题型:
如图,2条直线相交所组成的角中,互为对顶角的 角有2对:
角有2对: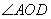 和
和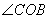 ,
,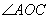 和
和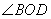 .
.
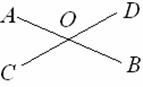
(1)3条直线相交于一点所组成的角中,互为对顶角的角有________________对;
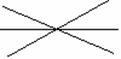
(2)4条直线相交于一点所组成的 角中,互为对顶角的角有________________对;
角中,互为对顶角的角有________________对;
(3)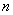 条直线相交于一点所组成的角中,互为对顶角的角有________________对.
条直线相交于一点所组成的角中,互为对顶角的角有________________对.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y= x的图象的交点
x的图象的交点 为C(m,4).
为C(m,4).
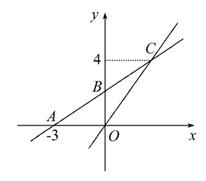
(1)求一次函数y=kx+b的解析式.
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
某企业对自己生产的某种产品进行市场调查,得出这种产品的市场需求量y(千件)和单价x(元)之间的关系式是y=15-3x.
(1)单价为2元时,市场需求量是 千件.
(2)如果单价为5元,那么可能出现的情况是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
已知一次函数y=kx-4,当x=2时,y=-3.
(1)求一次函数的解析式.
(2)将该函数的图象向上平移6个单位,求平移后的图象与x轴交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
由( )2=a(a≥0)可得a=(
)2=a(a≥0)可得a=( )2(a≥0),利用a=(
)2(a≥0),利用a=( )2(a≥0)可将任意一个非负数写成一个非负数的平方的形式,例如,3=(
)2(a≥0)可将任意一个非负数写成一个非负数的平方的形式,例如,3=( )2.参考以上方法在实数范围内分解因式:
)2.参考以上方法在实数范围内分解因式:
(1)x4-25. (2)2a2-7.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com