
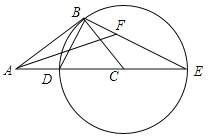
【题目】如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
(1)求证:△ABD∽△AEB;
(2)当![]() 时,求tanE;
时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=2,求⊙C的半径.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)要证明△ABD∽△AEB,已经有一组对应角是公共角,只需要再找出另一组对应角相等即可.
(2)由于AB:BC=4:3,可设AB=4,BC=3,求出AC的值,再利用(1)中结论可得AB2=ADAE,进而求出AE的值,所以tanE=![]() ;
;
(3)设设AB=4x,BC=3x,由于已知AF的值,构造直角三角形后利用勾股定理列方程求出x的值,即可知道半径3x的值.
试题解析:(1)∵∠ABC=90°,∴∠ABD=90°﹣∠DBC,由题意知:DE是直径,∴∠DBE=90°,∴∠E=90°﹣∠BDE,∵BC=CD,∴∠DBC=∠BDE,∴∠ABD=∠E,∵∠A=∠A,∴△ABD∽△AEB;
(2)∵AB:BC=4:3,∴设AB=4,BC=3,∴AC=![]() =5,∵BC=CD=3,∴AD=AC﹣CD=5﹣3=2,由(1)可知:△ABD∽△AEB,∴
=5,∵BC=CD=3,∴AD=AC﹣CD=5﹣3=2,由(1)可知:△ABD∽△AEB,∴![]() ,∴
,∴![]() =ADAE,∴
=ADAE,∴![]() =2AE,∴AE=8,在Rt△DBE中
=2AE,∴AE=8,在Rt△DBE中
tanE=![]() =
=![]() =
=![]() ;
;
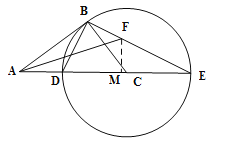
(3)过点F作FM⊥AE于点M,∵AB:BC=4:3,∴设AB=4x,BC=3x,∴由(2)可知;AE=8x,AD=2x,∴DE=AE﹣AD=6x,∵AF平分∠BAC,∴![]() ,∴
,∴![]() ,∵tanE=
,∵tanE=![]() ,∴cosE=
,∴cosE=![]() ,sinE=
,sinE=![]() ,∴
,∴![]() ,∴BE=
,∴BE=![]() ,∴EF=
,∴EF=![]() BE=
BE=![]() ,∴sinE=
,∴sinE=![]() =
=![]() ,∴MF=
,∴MF=![]() ,∵tanE=
,∵tanE=![]() ,∴ME=2MF=
,∴ME=2MF=![]() ,∴AM=AE﹣ME=
,∴AM=AE﹣ME=![]() ,∵
,∵![]() ,∴
,∴![]() ,∴x=
,∴x=![]() ,∴⊙C的半径为:3x=
,∴⊙C的半径为:3x=![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.一组邻边相等的矩形是正方形
B.对角线互相垂直的矩形是正方形
C.对角线相等的菱形是正方形
D.有一组邻边相等、一个角是直角的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
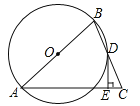
【题目】如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月24日是中国航天日.1970年的这一天,我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射,标志着中国从此进入了太空时代,它的运行轨道,距地球最近点439000米,将439000用科学记数法表示应为( )
A.0.439×106B.4.39×106C.4.39×105D.439×103
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com