
分析 (1)求出根的判别式,即可得出答案;
(2)先化成顶点式,根据顶点坐标和平移的性质得出即可;
(3)把y=4代入抛物线解析式,求出对应自变量x的值,即可求出MN的长度.
解答 解:(1)证明:∵△=(-2m)2-4×1×(m2+3)=4m2-4m2-12=-12<0,
∴方程x2-2mx+m2+3=0没有实数解,
即不论m为何值,该函数的图象与x轴没有公共点;
(2)y=x2-2mx+m2+3=(x-m)2+3,
把函数y=(x-m)2+3的图象沿y轴向下平移3个单位长度后,得到函数y=(x-m)2的图象,它的顶点坐标是(m,0),这个函数的图象与x轴只有一个公共点,
所以把函数y=x2-2mx+m2+3的图象向下平移3个单位长度后,得到的函数的图象与x轴只有一个公共点.
(3)(x-m)2+3=4,x1=m+1,x2=m-1,
MN=x1-x2=(m+1)-(m-1)=2.
点评 本题考查了二次函数和x轴的交点问题,根的判别式,平移的性质,二次函数的图象与几何变换的应用,主要考查学生的理解能力和计算能力,题目比较好,有一定的难度.


科目:初中数学 来源: 题型:解答题
 在Rt△ABC中,∠A=90°.
在Rt△ABC中,∠A=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF.
如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④DA平分∠CDE;⑤S△ABD:S△ACD=AB:AC.其中,正确的有5个.
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④DA平分∠CDE;⑤S△ABD:S△ACD=AB:AC.其中,正确的有5个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
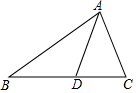 如图,D是△ABC的边BC上任一点,已知AB=4,AD=2,∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为$\frac{1}{3}$a.
如图,D是△ABC的边BC上任一点,已知AB=4,AD=2,∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为$\frac{1}{3}$a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com