
 如图,正方形ABCD中,点P,Q分别为AD,CD边上的点,且DQ=CP,连接BQ,AP.求证:BQ=AP.
如图,正方形ABCD中,点P,Q分别为AD,CD边上的点,且DQ=CP,连接BQ,AP.求证:BQ=AP. 科目:初中数学 来源: 题型:解答题
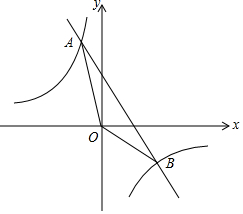 如图,已知一次函数y=-2x+3与反比例函数的图象相交于A(-1,m)、B(n,-2)两点.
如图,已知一次函数y=-2x+3与反比例函数的图象相交于A(-1,m)、B(n,-2)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 起步价:3公里以内9元(不再收取燃油附加税) 每公里价格:超过3公里部分,2元/公里(不足1公里按1公里算) 空驶补贴费:超过12公里以上部分,每公里加收公里运价的50% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
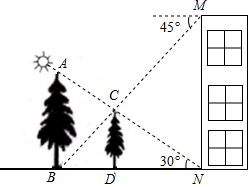 如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB、CD的高度.(结果保留根号)
如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB、CD的高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
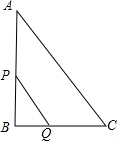 如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.
如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com