
【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据: ![]() ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).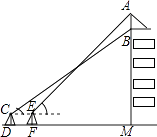
【答案】解:过点C作CN⊥AM于点N,则点C,E,N在同一直线上,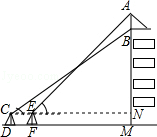
设AB=x米,则AN=x+(17﹣1)=x+16(米),
在Rt△AEN中,∠AEN=45°,
∴EN=AN=x+16,
在Rt△BCN中,∠BCN=37°,BM=17,
∴tan∠BCN= ![]() =0.75,
=0.75,
∴ ![]() =
= ![]() ,
,
解得:x=1 ![]() ≈1.3.
≈1.3.
经检验:x=1 ![]() 是原分式方程的解
是原分式方程的解
【解析】首先过点C作CN⊥AM于点N,则点C,E,N在同一直线上,设AB=x米,则AN=x+(17﹣1)=x+16(米),则在Rt△AEN中,∠AEN=45°,可得EN=AN=x+16,在Rt△BCN中,∠BCN=37°,BM=17,可得tan∠BCN= ![]() =0.75,则可得方程:
=0.75,则可得方程: ![]() ,解此方程即可求得答案.
,解此方程即可求得答案.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E. 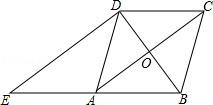
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y= ![]() 的图象上,OA=2,OC=6,则正方形ADEF的边长为 .
的图象上,OA=2,OC=6,则正方形ADEF的边长为 . 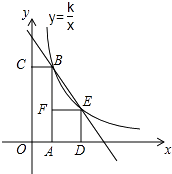
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC. 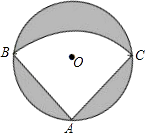
(1)求被剪掉阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1 , y1),B(x2 , y2),AB中点P的坐标为(xp , yp).由xp﹣x1=x2﹣xp , 得xp= ![]() ,同理yp=
,同理yp= ![]() ,所以AB的中点坐标为(
,所以AB的中点坐标为( ![]() ,
, ![]() ).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A、B两点间的距离公式为AB=
).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A、B两点间的距离公式为AB= ![]() .这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
.这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题: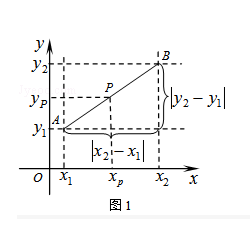
(1)已知M(1,﹣2),N(﹣1,2),直接利用公式填空:MN中点坐标为 , MN= .
(2)如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.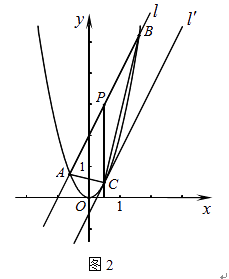
(a)求A、B两点的坐标及C点的坐标;
(b)连结AB、AC,求证△ABC为直角三角形;
(c)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解南山荔枝的销售情况,某部门对该市场的三种荔枝品种A,B,C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整),请你结合图中的信息,解答下列问题: 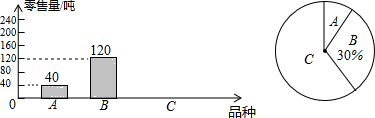
(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)补全图1的统计图并计算图2中A所在扇形的圆心角的度数;
(3)某商场计划六月下半月进货A、B、C三种荔枝共300千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF. 
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com