
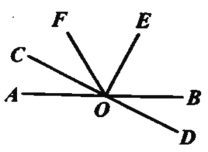
【题目】如图所示,已知直线![]() 和
和![]() 相交于点
相交于点![]() .
.![]() 是直角,
是直角,![]() 平分
平分![]() .
.
(1)![]() 与
与![]() 的大小关系是 ,判断的依据是 ;
的大小关系是 ,判断的依据是 ;
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)相等,同角的补角相等;(2)26°
【解析】
(1)根据对顶角相等填空即可;
(2)首先根据直角由已知角求得它的余角,再根据角平分线的概念求得∠AOE,再利用角的关系求得∠AOC,根据上述结论,即求得了∠BOD.
解:(1)相等;同角的补角相等 (对顶角相等).
(2)∵∠COE=90°,∠COF=32°
∴∠EOF=∠COE-∠COF=90°-32°=58°
∵OF平分∠AOE
∴∠AOF=∠EOF=58°
∴∠AOC=∠AOF-∠COF=58°-32°=26°
∵∠AOC+∠BOC=180°
∠BOD+∠BOC=180°
∴∠BOD=∠AOC=26°
或∵∠COE=90°,∠COF=32°
∴∠EOF=∠COE-∠COF=90°-32°=58°
∵OF平分∠AOE
∴∠AOE=2∠EOF=116°
∴∠EOB=180°-∠AOE = 64°
∵∠EOD=180°-∠COE=90°
∴∠BOD=∠EOD - ∠EOB=26°


科目:初中数学 来源: 题型:
【题目】如图,点![]() 为线段
为线段![]() 上一点,点
上一点,点![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() .
.
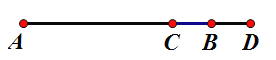
(1)图中共有______条线段,分别是______;
(2)求线段![]() 的长;
的长;
(3)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
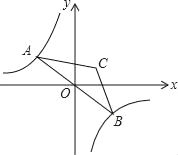
【题目】如图,点A是双曲线y=﹣![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() 上运动,则k的值为_____.
上运动,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的二次函数y=ax2﹣bx+2(a≠0).
(1)当a=﹣2,b=﹣4时,求该函数图象的对称轴及顶点坐标.
(2)在(1)的条件下,Q(m,t)为该函数图象上的一点,若Q关于原点的对称点P也落在该函数图象上,求m的值.
(3)当该函数图象经过点(1,0)时,若A(![]() ,y1),B(
,y1),B(![]() ,y2)是该函数图象上的两点,试比较y1与y2的大小.
,y2)是该函数图象上的两点,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
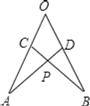
【题目】如图,在∠AOB的两边截取OA=OB,OC=OD,连接AD,BC交于点P,则下列结论中①△AOD≌△BOC,②△APC≌△BPD,③点P在∠AOB的平分线上.正确的是__.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种饮料由A、B两种原液按一定比例配制而成,其中A原液成本价为10元/千克,B原液为15元/千克,按现行价格销售每千克获得60%的利润率.由于物价上涨,A原液上涨20%,B原液上涨10%,配制后的总成本增加15%,公司为了拓展市场,打算再投入现行总成本的25%做广告宣传,使得销售成本再次增加,如果要保证每千克的利润率不变,则此时这种饮料的售价与原售价之差为_____元/千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴子A、B两点,与反比例函数y![]() 的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
(1)求反比例函数与一次函数的关系式;
(2)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,数轴上两点A,B表示的数分别是9和-6,动点P从点A出发,以每秒3个单位的速度沿数轴向点B运动,运动到点B停止;
(1)在数轴上表示出A,B两点,并直接回答:线段AB的长度是 ;
(2)若满足BP=2AP,求点P的运动时间;
(3)在点P运动过程中,若点M为线段AP的中点,点N为线段BP的中点,请计算线段MN的长度,并说出线段MN与线段AB的数量关系;
(4)若另一动点Q同时从B点出发,运动的速度是每秒2个单位,几秒钟后,线段PQ长度等于5?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com