
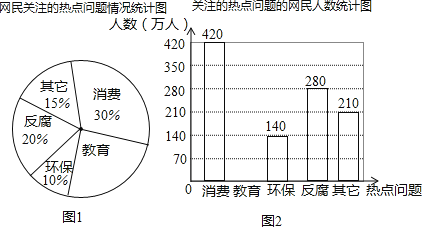
【题目】某调查机构将今年绍兴市民最关注的热点话题分为消费.教育.环保.反腐及其它共五类.根据最近一次随机调查的相关数据,绘制的统计图表如下:
根据以上信息解答下列问题:
(1)本次共调查_________人,请在答题卡上补全条形统计图并标出相应数据;
(2)若绍兴市约有500万人口,请你估计最关注教育问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲.乙.丙.丁四人最关注教育问题,现准备从这四中随机抽取两人进行座谈,求抽取的两人恰好是甲和乙的概率(画树状图或列表说明).
科目:初中数学 来源: 题型:
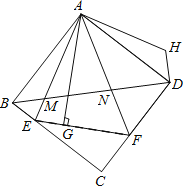
【题目】如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.
(1)求证:四边形ABCD是正方形;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)若EG=4,GF=6,BM=3![]() ,求AG、MN的长.
,求AG、MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为2m,宽为1.2m的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
(1)若长方体底面面积为1.28m2,求裁掉的正方形边长;
(2)若要求制作的长方体的底面长不大于底面宽的3倍,并将容器进行防锈处理,侧面每平方米的费用为50元,底面每平方米的费用为200元,裁掉的正方形边长多大时,总费用最低,最低为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
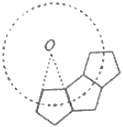
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”,在Rt△ABC中,∠ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,BM的长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
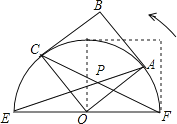
【题目】如图,正方形OABC的边长为6,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
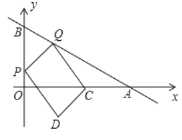
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别角与A、B两点,P、Q分别是线段OB、AB上的两个动点,点P从O出发一每秒2个单位长度的速度向终点B运动,同时Q从B出发,以每秒5个单位的速度向终点A运动,当其中一点到达终点时整个运动结束,设运动时间为t秒。
轴分别角与A、B两点,P、Q分别是线段OB、AB上的两个动点,点P从O出发一每秒2个单位长度的速度向终点B运动,同时Q从B出发,以每秒5个单位的速度向终点A运动,当其中一点到达终点时整个运动结束,设运动时间为t秒。
(1)求出点Q的坐标(用t的代数式表示)
(2)若C为OA的中点,连接PQ、CQ,以PQ、CQ为邻边作![]() PQCD.
PQCD.
①是否存在时间t,使得坐标轴切好将![]() PQCD的面积分为1:5的两个部分,若存在,求出t的值;若不存在,请说明理由.
PQCD的面积分为1:5的两个部分,若存在,求出t的值;若不存在,请说明理由.
②直接写出整个运动过程中![]() PQCD对角线DQ的取值范围.
PQCD对角线DQ的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 与正方形
与正方形![]() 共顶点
共顶点![]() .
.
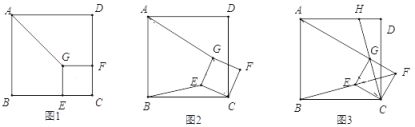
(1)探究:如图,点![]() 在正方形
在正方形![]() 的边
的边![]() 上,点
上,点![]() 在正方形
在正方形![]() 的边
的边![]() 上,连接
上,连接![]() .求证:
.求证:![]() ;
;
(2)拓展:将如图中正方形![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 角
角![]() ,如图所示,试探究线段
,如图所示,试探究线段![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)运用:正方形![]() 在旋转过程中,当
在旋转过程中,当![]() ,
,![]() ,
,![]() 三点在一条直线上时,如图所示,延长
三点在一条直线上时,如图所示,延长![]() 交
交![]() 于点
于点![]() .若
.若![]() ,GH=2
,GH=2![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com