
【题目】如图,一条直线y1=klx+b与反比例函数y2= ![]() 的图象交于A(1,5)、B(5,n)两点,与x轴交于C点,
的图象交于A(1,5)、B(5,n)两点,与x轴交于C点, 
(1)求反比例函数的解析式;
(2)求C点坐标;
(3)请直接写出当y1<y2时,x的取值范围.
【答案】
(1)解:∵反比例函数y2= ![]() 的图象过点A(1,5),
的图象过点A(1,5),
∴k2=1×5=5,
∴反比例函数的解析式为y2= ![]()
(2)解:∵反比例函数y2=⌒的图象过点B(5,n),
∴n= ![]() =1,
=1,
∴B(5,1).
将A(1,5),B(5,1)代入y1=klx+b,
得 ![]() ,解得
,解得 ![]() ,
,
∴直线的解析式为y1=﹣x+6,
∴C点的坐标是(6,0)
(3)解:观察函数图象可知:当0<x<1或x>5时,一次函数的图象在反比例函数图象的下方,
∴当y1<y2时,x的取值范围是0<x<1或x>5
【解析】(1)由A与B为一次函数与反比例函数的交点,将A坐标代入反比例函数解析式中,求出k2的值,确定出反比例解析式;(2)将B的坐标代入反比例解析式中求出n的值,确定出B的坐标,将A、B两点的坐标代入一次函数解析式中求出k1和b的值,确定出直线的解析式,进而求出C点坐标;(3)根据图象,结合交点坐标即可求解.


科目:初中数学 来源: 题型:
【题目】已知:△ABC≌△DEF,AB=DE,∠A=70°,∠E=30°,则∠F的度数为()
A. 80° B. 70° C. 30° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初级中学正在开展 “文明城市创建人人参与,志愿服务我当先行”的“创文活动”.为了了解该校志愿者参与服务情况,现对该校全体志愿者进行随机抽样调查.根据调查数据绘制了如下所示不完整统计图.条形统计图中七年级、八年级、九年级、教师分别指七年级、八年级、九年级、教师志愿者中被抽到的志愿者,扇形统计图中的百分数指的是该年级被抽到的志愿者数与样本容量的比.
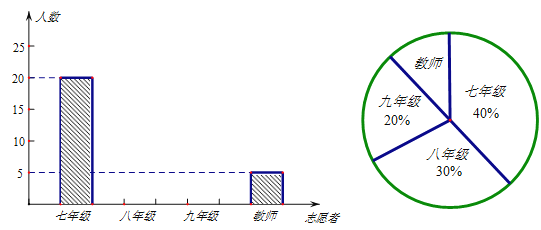
(1)请补全条形统计图;
(2)若该校共有志愿者600人,则该校七年级大约有多少志愿者?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在“元旦”促销期间规定:超市内所有商品按标价的![]() 出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:
出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:
消费金额 |
|
|
|
获得奖券金额(元) |
|
|
|
(符号![]() 表示
表示![]() 是大于或等于
是大于或等于![]() ,而小于
,而小于![]() 的数)
的数)
根据上述促销方法知道,顾客在超市内购物可以获得双重优惠,即顾客在超市内购物获得的优惠额![]() 商品的折扣
商品的折扣![]() 相应的奖券金额,例如:购买标价为
相应的奖券金额,例如:购买标价为![]() 元的商品,则消费金额为:
元的商品,则消费金额为: ![]() 元,获得的优惠额为:
元,获得的优惠额为: ![]() 元.
元.
(![]() )购买一件标价为
)购买一件标价为![]() 元的商品,求获得的优惠额.
元的商品,求获得的优惠额.
(![]() )对于标价在
)对于标价在![]() 元与
元与![]() 元之间(含
元之间(含![]() 元和
元和![]() 元)的商品,顾客购买标价为多少元的商品时可以得到
元)的商品,顾客购买标价为多少元的商品时可以得到![]() 的优惠率.(设购买该商品得到的优惠率
的优惠率.(设购买该商品得到的优惠率![]() 购买商品获得的优惠额
购买商品获得的优惠额![]() 商品的标价)
商品的标价)
查看答案和解析>>
科目:初中数学 来源: 题型:
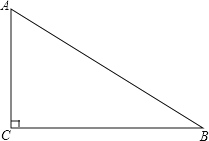
【题目】如图,在△ABC中,∠C=90°,∠B=30°.
(1)作∠A的平分线AD,交BC于点D(用尺规作图,不写作法,但保留作图痕迹,然后用墨水笔加黑);
(2)计算S△DAC:S△ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F. 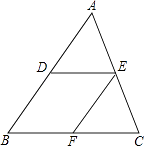
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com