
 已知反比例函数
已知反比例函数 与一次函数图象交于P(-2,1)和Q(1,n)两点.
与一次函数图象交于P(-2,1)和Q(1,n)两点. 得k=-2×1=-2,
得k=-2×1=-2,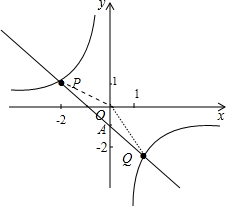
 ;
; 得n=-2,
得n=-2,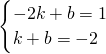 ,解得
,解得 ,
, ×1×1+
×1×1+ ×1×2=
×1×2= .
. 可得k=-2×1=-2,则确定了反比例函数解析式为y=-
可得k=-2×1=-2,则确定了反比例函数解析式为y=- ;再把Q(1,n)代入y=-
;再把Q(1,n)代入y=- 得确定Q点坐标为(1,-2),然后利用待定系数法确定过P、Q两点的一次函数解析式;
得确定Q点坐标为(1,-2),然后利用待定系数法确定过P、Q两点的一次函数解析式;

科目:初中数学 来源: 题型:阅读理解
| 周数x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 销售量y(件) | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| x | 3O00 | 3200 | 3500 | 4000 |
| y | 100 | 96 | 90 | 80 |
| 租出的车辆数 | -
-
|
未租出的车辆数 |
| ||||||||
| 租出每辆车的月收益 | x-150 x-150 |
所有未租出的车辆每月的维护费 | x-3000 x-3000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 销售价x(元/千克) | 21 | 23 | 25 | 27 |
| 销售量w(千克) | 38 | 34 | 30 | 26 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 月份x(月) | 1 | 2 | 3 | 4 | 5 | … |
| “绿色健康”食品产量y(吨) | 48 | 46 | 44 | 42 | 40 | … |
| 11 |
| 12 |
| 13 |
| 14 |
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(山东莱芜卷)数学 题型:解答题
(本小题满分12分)已知反比例函数 和一次函数
和一次函数 ,其中一次
,其中一次
函数图象经过(a,b)与(a+1,b+k)两点.

(1) 求反比例函数的解析式.
(2) 如图,已知点A是第一象限内上述两个函数图象的交点,求A点坐标.
(3) 利用(2)的结果,请问:在X轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com