
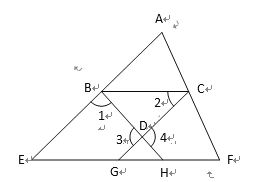
【题目】如图,已知∠1+∠4﹦180°,∠2﹦∠E,则EF∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.
证明:
∵∠1+∠4﹦180°( ),
∠3﹦∠4 ( ),
∴∠1﹢ ﹦180°.
∴AE∥CG ( )
∴∠E﹦∠CGF( ).
∵∠2﹦∠E(已知)
∴ ∠2﹦∠CGF( ).
∴ BC∥EF( ).
【答案】对顶角相等;∠3;同旁内角互补,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行
【解析】
根据对顶角相等,得出∠3=∠4,根据等量代换可知∠1+∠3=180°,根据同旁内角互补,两直线平行,得出AE∥CG,再由两直线平行,同位角相等,得出∠E=∠CGF,已知∠2=∠E,由等量代换可知∠2=∠CGF,再根据内错角相等,两直线平行,即可得出EF∥BC.
证明:∵∠1+∠4﹦180(已知),
∠3﹦∠4 ( 对顶角相等 ),
∴∠1﹢∠3﹦180°.
∴AE∥CG ( 同旁内角互补,两直线平行)
∴∠E﹦∠CGF(两直线平行,同位角相等 ).
∵∠2﹦∠E(已知)
∴ ∠2﹦∠CGF( 等量代换 ).
∴ BC∥EF(内错角相等,两直线平行).


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
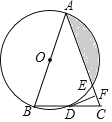
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
(1)若⊙O的半径为3,∠CDF=15°,求阴影部分的面积;
(2)求证:DF是⊙O的切线;
(3)求证:∠EDF=∠DAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
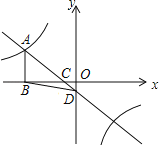
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.
(1)求一次函数和反比例函数的解析式;
(2)若直线AC与y轴交于点D,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,∠ABC=35°,E是BC边上一点且AE=CE,D是
BC边上的中点,连接AD,AE.
(1)求∠DAE的度数;
(2)若BD上存在点F,且∠AFE=∠AEF,求证:BF=CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
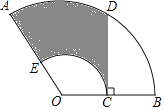
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )
A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
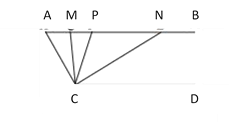
【题目】如图,已知AB∥CD,∠A=40°,点P是射线B上一动点(与点A不重合),CM,CN分别平分∠ACP和∠PCD,分别交射线AB于点M,N.
(1)求∠MCN的度数.
(2)当点P运动到某处时,∠AMC=∠ACN,求此时∠ACM的度数.
(3)在点P运动的过程中,∠APC与∠ANC的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
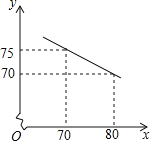
【题目】为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业,王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价x(元)和游客居住房间数y(间)的信息,乐乐绘制出y与x的函数图象如图所示:
(1)求y与x之间的函数关系式;
(2)合作社规定每个房间价格不低于60元且不超过150元,对于游客所居住的每个房间,合作社每天需支出20元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加2m/s.
(1)求小球速度v(单位:m/s)关于时间t(单位:s)的函数解析式,它是一次函数吗?
(2)求第3.5s时小球的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,请用直尺和圆规依次完成下列操作.
(1)在线段 AC 上找一点 M,使点 M 到 AB 和 BC 的距离相等;
(2)在射线 BM 上找一点 N,使 NB=NC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com