设[x]表示不小于x的最小整数.如[3.6]=4.[-2]=-2.则[-2.8]-[5]=-7．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

3．设[x]表示不小于x的最小整数，如[3.6]=4，[-2]=-2，则[-2.8]-[5]=-7．

分析利用题中的新定义求出各自的值，计算即可得到结果．

解答解：根据题意得：[-2.8]-[5]=-2-5=-7，
故答案为：-7

点评此题考查了有理数的大小比较，弄清题中的新定义是解本题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

18．已知x，y是有理数，y≠0，并且满足x²+2y+$\sqrt{2}$y=17-4$\sqrt{2}$，求x、y的值．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

14．

如图，∠AOB=120°，AO⊥DO，BO⊥CO，则∠COD的度数是（　　）

A．

60°

B．

45°

C．

40°

D．

30°

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

11．有一个运算程序，可以使：a⊕b=n（n为常数）时，得（a+1）⊕b=n+1，a⊕（b+1）=n-2，现在已知1⊕1=2，那么2019⊕2019=-2016．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．解方程
（1）（3y-2）²=（2y-3）²
（2）（2x-1）²=3（1-2x）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．

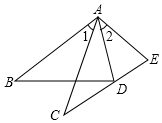在数学课上，林老师在黑板上画出如图所示的△ABD和△ACE两个三角形，并写出四个条件：①AB=AC；②AD=AE；③∠1=∠2；④∠B=∠C．请你从这四个条件中选出三个作为题设，另一个作为结论，组成一个真命题，并给予证明．
题设：①②③；
结论：④．（均填写序号）
证明：
∵∠1=∠2，
∴∠BAD=∠CAE．
在△ABD和△ACE中，$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠BAD=∠CAE}&{\;}\\{AD=AE}&{\;}\end{array}\right.$，
∴△ABD≌△ACE．（SAS），
∴∠B=∠C（全等三角形对应边相等）；．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．

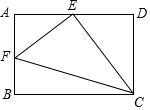如图，在矩形ABCD中，E是AD的中点，EF⊥EC交AB于点F，连接FC，问：△AEF与△ECF相似吗？若相似，探求你的结论，若不相似，请说明理由．