练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．

    下面有三个推断：
    ①当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；
    ②随着试验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；
    ③若再次用计算机模拟此实验，则当投掷次数为1000时，“钉尖向上”的频率一定是0.620．
    其中合理的是（　　）
    A．①B．②C．①②D．①③

    分析 根据图形和各个小题的说法可以判断是否正确，从而可以解答本题．

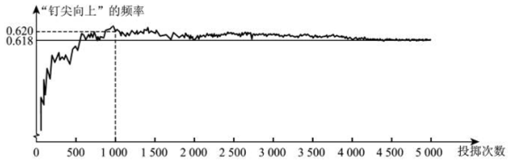
    解答 解：当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以此时“钉尖向上”的可能性是：308÷500=0.616，但“钉尖向上”的概率不一定是0.616，故①错误，
    随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618．故②正确，
    若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的概率可能是0.620，但不一定是0.620，故③错误，
    故选B．

    点评 本题考查利用频率估计概率，解答本题的关键是明确概率的定义，利用数形结合的思想解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

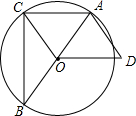    15．如图，已知△ABC内接于⊙O，AB是直径，OD∥AC，AD=OC．
    （1）当∠B=30°时，请判断四边形OCAD的形状，为什么？
    （2）当∠B等于多少度时，AD与⊙O相切？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

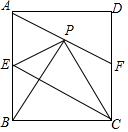    16．如图，在矩形ABCD中，点E为AB中点，连接EC，点P是点B关于直线EC的对称点，连结AP并延长交CD于点F，给出下列结论：①AF∥EC；②PE=DF；③若△PBC是等边三角形，则EC=AB；④若AB=30，BC=20，则AP=17．其中正确的结论有①②③．（把所有正确结论的序号都填上）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．求不等式组$\left\{\begin{array}{l}{3-x＜2x+10}\\{\frac{x}{2}-1≤\frac{x-2}{3}}\end{array}\right.$的所有整数解的和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．已知$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组$\left\{\begin{array}{l}{x-2y=0}\\{2x+y=5}\end{array}\right.$的解，则3a-b=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．已知关于x的不等式组$\left\{\begin{array}{l}{x≥a}\\{2x+1＜5}\end{array}\right.$ 只有两个整数解，则实数a的取值范围是-1＜a≤0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

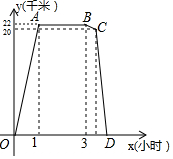    17．某周日上午8：00小宇从家出发，乘车1小时到达某活动中心参加实践活动．11：00时他在活动中心接到爸爸的电话，因急事要求他在12：00前回到家，他即刻按照来活动中心时的路线，以5千米/小时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家x（小时）后，到达离家y（千米）的地方，图中折线OABCD表示y与x之间的函数关系．
    （1）活动中心与小宇家相距22千米，小宇在活动中心活动时间为2小时，他从活动中心返家时，步行用了0.4小时；
    （2）求线段BC所表示的y（千米）与x（小时）之间的函数关系式（不必写出x所表示的范围）；
    （3）根据上述情况（不考虑其他因素），请判断小宇是否能在12：00前回到家，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

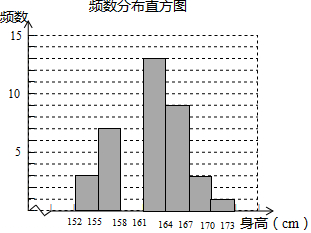    14．某体育老师测量了自己任教的甲、乙两班男生的身高，并制作了如下不完整的统计图表．
     身高分组 频数 频率
     152≤x＜155 3 0.06
     155≤x＜158 7 0.14
     158≤x＜161 m 0.28
     161≤x＜164 13 n
     164≤x＜167 9 0.18
     167≤x＜170 3 0.06
     170≤x＜173 1 0.02
    根据以上统计图表完成下列问题：
    （1）统计表中m=14，n=0.26，并将频数分布直方图补充完整；
    （2）在这次测量中两班男生身高的中位数在：161≤x＜164范围内；
    （3）在身高≥167cm的4人中，甲、乙两班各有2人，现从4人中随机推选2人补充到学校国旗护卫队中，请用列表或画树状图的方法求出这两人都来自相同班级的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．一条小船沿直线向码头匀途前进，在0min，2min，4min，6min时，测得小船与码头的距离分别为200m，150m，100m，50m，小船与码头的距离s是时间t的函数吗？如果是，写出函数解析式，并画出函数图象，如果船速不变，多长时间后小船到达码头？

    查看答案和解析>>

    同步练习册答案