练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD=BC，∠FPE=100°，则∠PFE的度数是40°．

    分析 根据三角形中位线定理得到EP=$\frac{1}{2}$AD，FP=$\frac{1}{2}$BC，得到PE=PF，根据等腰三角形的性质、三角形内角和定理计算即可．

    解答 解：∵P是对角线BD的中点，E是AB的中点，
    ∴EP=$\frac{1}{2}$AD，
    同理，FP=$\frac{1}{2}$BC，
    ∵AD=BC，
    ∴PE=PF，
    ∵∠FPE=100°，
    ∴∠PFE=40°，
    故答案为：40°．

    点评 本题考查的是三角形中位线定理的应用，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．如图，⊙O的直径CD=8，AB是⊙O的弦，AB⊥CD于M，且CM=2，则AB的长为4$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．关于x的方程a（x+m）2+b=0的解是x1=-2，x2=1（a，m，b为常数，a≠0），则a（x+m+6）2+b=0的解是x=-8或x=-5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

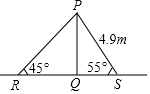    4．图中，PQ为一直立旗杆，PR及PS为两条已拉紧的绳，以将该旗杆固定在水平地面RQS上，PS的长度为4.9m，由R及S测得P的仰角分别为45°及55°．利用正弦公式，求R与S之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．一次函数y1=kx+3与正比例函数y2=-2x交于点A（-1，2）．
    （1）确定一次函数表达式；
    （2）当x取何值时，y1＜0？
    （3）当x取何值时，y1＞y2？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

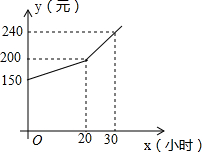    1．为了鼓励小强做家务，小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的．若设小强每月的家务劳动时间为x小时，该月可得（即下月他可获得）的总费用为y元，则y（元）和x（小时）之间的函数图象如图所示．
    （1）根据图象，分别写出当0≤x≤20与x＞20时．y关于x的函数关系式．
    （2）若小强希望下个有250元费用，则小强本月需做家务多少时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，已知OA=OB．
    （1）说出数轴上点A所表示的数；
    （2）比较点A所表示的数与-3.2的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图所示，炮兵在地面C点观察到空中B点有一架敌机，仰角为45°，敌机在同一高度作直线飞行，经过D点到达A点时炮兵观测的仰角为30°，而D点位于炮兵阵地C的正上方2000米处，该敌机从B点飞到A点用1分钟，求敌机的飞行速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．定义：如果以三个正数为边长，能组成一个直角三角形，则称这三个数字为一组“毕氏数”，记为（a，b，c），其中a≤b＜c，如（6，8，10），（8，15，17），（1，$\sqrt{2}，\sqrt{3}$），（5，12，13），（1，1，$\sqrt{2}$），（14，48，50），（9，12，15），（20，21，29）等，如果一组“毕氏数”均为整数，且公因数只有1，则称这组“毕氏数”为“素毕氏数”，请写出一组“素毕氏数”，且满足c＞100，你是怎么想到的？请说明你的思路．

    查看答案和解析>>

    同步练习册答案