
【题目】在平面直角坐标系中,已知A(0,a)、B(b, 0),且a、b满足: ![]() ,点D为x正半轴上一动点
,点D为x正半轴上一动点
(1)求A、B两点的坐标
(2)如图,∠ADO的平分线交y轴于点C,点 F为线段OD上一动点,过点F作CD的平行线交y轴于点H,且∠AFH=45°, 判断线段AH、FD、AD三者的数量关系,并予以证明

(3)以AO为腰,A为顶角顶点作等腰△ADO,若∠DBA=30°,直接写出∠DAO的度数

科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道:点A.B在数轴上分别表示有理数a、b,A.B两点之间的距离表示为AB,在数轴上A.B两点之间的距离AB=|a-b|.所以式子|x3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,解答下列问题:
![]()
(1)若|x3|=4,则x=______;
(2)式子|x3|=|x+1|,则x=______;
(3)若|x3|+|x+1|=9,借助数轴求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D. E(点A. E位于点B的两侧),满足BP=BE,连接AP、CE.
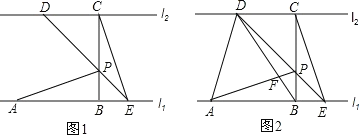
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F. 如图2.
①当![]() =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;
②当![]() =n(n>1)时,设△DAP的面积为S1,△EPC的面积为S2,求
=n(n>1)时,设△DAP的面积为S1,△EPC的面积为S2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府于2017年初投资了112万元,建成40个公共自行车站点、配置720辆公共自行车正式启用公共自行车租贷系统:今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2019年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)每个站点的造价和公共自行车的单价分别是多少万元?
(2)若2017年到2019年市政府配置公共自行车数量的年平均增长率相同,请你求出2018年市政府配置公共自行车的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点D、E分别是△ABC两边AB、BC所在直线上的点,∠BDE+∠ACB=180°,DE=AC,AD=2BD.


(1) 如图1,当点D、E分别在AB、CB的延长线上时,求证:BE=BD
(2) 如图2,当点D、E分别在AB、BC边上时,BE与BD存在怎样的数量关系?请写出你的结论,并证明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司计划购买A型和B型两种货车共8辆,其中每辆车的价格以及每辆车的运载量如下表:
A型 | B型 | |
价格(万元/台) | m | n |
运载量(吨/车) | 20 | 30 |
若购买A型货车1辆,B型货车3辆,共需67万元;若购买A型货车3辆,B型货车2辆,共需75万元.
(1)求m,n的值;
(2)若每辆A型货车每月运载量500吨,每辆B型货车每月运载量750吨,为确保这8辆车每月的运载量总和不少于4750吨,且该公司购买A型和B型货车的总费用不超过124万元.请你设计一个方案,使得购车总费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 是⊙M 的直径,BC 是⊙M 的切线,切点为 B,C 是 BC 上(除 B 点外)的任意一点,连接 CM 交⊙M 于点 G,过点 C 作 DC⊥BC 交 BG 的 延长线于点 D,连接 AG 并延长交 BC 于点 E.
(1)求证:△ABE∽△BCD;
(2)若 MB=BE=1,求 CD 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 延长线上的一点,点
延长线上的一点,点![]() 是
是![]() 的中点。
的中点。

(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法)。
①作![]() 的平分线
的平分线![]() . ②连接
. ②连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(2)猜想与证明:试猜想![]() 与
与![]() 有怎样的关系,并说明理由。
有怎样的关系,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com