
【题目】如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
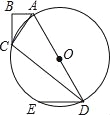
(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
【答案】(1)详见解析;(2)![]() ;(3)圆心O到弦ED的距离为
;(3)圆心O到弦ED的距离为![]() .
.
【解析】
试题分析:(1)如图1,连结CO.先由勾股定理求出AC=10,再利用勾股定理的逆定理证明△ACD是直角三角形,∠C=90°,那么OC为Rt△ACD斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半得出OC=![]() AD=r,即点C在圆O上;(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB=
AD=r,即点C在圆O上;(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB=![]() =
=![]() ,则tan∠CDE=tan∠ACB=
,则tan∠CDE=tan∠ACB=![]() ;(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=
;(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=![]() AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF=
AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF=![]() ,那么BF=BC+CF=
,那么BF=BC+CF=![]() .再证明四边形ABFE是矩形,得出AE=BF=
.再证明四边形ABFE是矩形,得出AE=BF=![]() ,所以OG=
,所以OG=![]() AE=
AE=![]() .
.
试题解析:(1)证明:如图1,连结CO.
∵AB=6,BC=8,∠B=90°,
∴AC=10.
又∵CD=24,AD=26,102+242=262,
∴△ACD是直角三角形,∠C=90°.
∵AD为⊙O的直径,
∴AO=OD,OC为Rt△ACD斜边上的中线,
∴OC=![]() AD=r,
AD=r,
∴点C在圆O上;
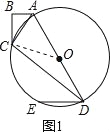
(2)解:如图2,延长BC、DE交于点F,∠BFD=90°.
∵∠BFD=90°,
∴∠CDE+∠FCD=90°,
又∵∠ACD=90°,
∴∠ACB+∠FCD=90°,
∴∠CDE=∠ACB.
在Rt△ABC中,tan∠ACB=![]() =
=![]() ,
,
∴tan∠CDE=tan∠ACB=![]() ;
;
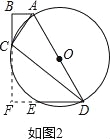
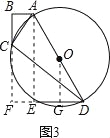
(3)解:如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=![]() AE.
AE.
易证△ABC∽△CFD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CF=![]() ,
,
∴BF=BC+CF=8+![]() =
=![]() .
.
∵∠B=∠F=∠AED=90°,
∴四边形ABFE是矩形,
∴AE=BF=![]() ,
,
∴OG=![]() AE=
AE=![]() ,
,
即圆心O到弦ED的距离为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
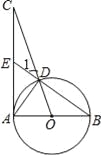
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
(1)-个数不是正数就是负数;
(2)海拔-155米表示比海平面低155米;
(3)温度0℃就是没有温度;
(4)零是最小的数;
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五月初,我市多地遭遇了持续强降雨的恶劣天气,造成部分地区出现严重洪涝灾害,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共2000件送往灾区,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用350元购买甲种物品的件数恰好与用300元购买乙种物品的件数相同
(1)求甲、乙两种救灾物品每件的价格各是多少元?
(2)经调查,灾区对乙种物品件数的需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水库的平均水位为80米,在此基础上,若水位变化时,把水位上升记为正数;水库管理员记录了3月~8月水位变化的情况(单位:米):-5,-4,0,+3,+6,+8.试问这几个月的实际水位是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某项工程由甲乙两队合作12天可以完成,供需工程费用13800元,乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多150元。
(1)甲乙两队单独完成这项工程分别需要多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成这项工程,从节约资金的角度考虑,应该选择哪个工程队?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com