
【题目】如图,在矩形ABCD中,E为边AB的中点,将△CBE沿CE翻折得到△CFE,连接AF,若∠EAF=70°,那么∠BCF=______度.

【答案】40
【解析】
由矩形的性质得出∠B=90°,由折叠的性质得出∠EFC=∠B=90°,∠FEC=∠CEB,∠FCE=∠BCE,FE=BE,证出AE=FE,由等腰三角形的性质得出∠EFA=∠EAF=70°,由三角形的外角性质求出∠BEF=∠EAF+∠EFA=140°,得出∠CEB=∠FEC=70°,由直角三角形的性质得出∠FCE=∠BCE=20°,即可得出答案.
∵四边形ABCD是矩形,
∴∠B=90°,
∵E为边AB的中点,
∴AE=BE,
由折叠的性质可得:∠EFC=∠B=90°,∠FEC=∠CEB,∠FCE=∠BCE,FE=BE,
∴AE=FE,
∴∠EFA=∠EAF=70°,
∴∠BEF=∠EAF+∠EFA=140°,
∴∠CEB=∠FEC=70°,
∴∠FCE=∠BCE=90°-70°=20°,
∴∠BCF=20°+20°=40°;
故答案为:40.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是

A. 当x=3时,EC<EM B. 当y=9时,EC>EM
C. 当x增大时,EC·CF的值增大。 D. 当y增大时,BE·DF的值不变。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图![]() 不完整
不完整![]() 根据统计图中的信息,若全校有2050名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生人数为
根据统计图中的信息,若全校有2050名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生人数为![]()

A.1330B.1350C.1682D.1850
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ.
(2)判断△APQ的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经收集整理后得下表:( )
班级 | 参加人数 | 中位数 | 平均数 | 方差 |
甲 | 55 | 149 | 135 | 191 |
乙 | 55 | 151 | 135 | 110 |
某同学根据上表分析得出如下结论:
(1)甲、乙两班学生成绩的平均水平相同;
(2)乙班优秀的人数多于甲班优秀的人数;(每分钟输入汉字![]() 个为优秀)
个为优秀)
(3)甲班成绩的波动情况比乙班成绩的波动小.
上述结论中正确的是( )
A.(1)(2)(3)B.(1)(2)C.(1)(3)D.(2)(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机械厂的总工程师张青家距厂部很远,每天都由厂部小客车接送,厂车到接送停靠站接到张青立即返程,根据厂车的出车时间和速度,张青总能算准时间,通常是他到停靠站时,厂车正好到达,这样,双方均不必等候.有一次,张青因挂念厂里的科研课题,提前80分钟到停靠站后没有等汽车,而是迎着厂车来的方向走去,遇到厂车后,他乘车到达厂部,结果比平时早20分,则汽车的速度是张青步行速度的______倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 三点在数轴上的位置如图所示,它们表示的数分别是
三点在数轴上的位置如图所示,它们表示的数分别是![]() ,
,![]() ,
,![]() .
.
![]()
(1)填空:![]() ______0,
______0,![]() ______0:(填“>”,“=”或“<”)
______0:(填“>”,“=”或“<”)
(2)若![]() 且点
且点![]() 到点
到点![]() ,
,![]() 的距离相等,
的距离相等,
①当![]() 时,求
时,求![]() 的值.
的值.
②![]() 是数轴上
是数轴上![]() ,
,![]() 两点之间的一个动点,设点
两点之间的一个动点,设点![]() 表示的数为
表示的数为![]() ,当
,当![]() 点在运动过程中,
点在运动过程中,![]() 的值保持不变,则
的值保持不变,则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对角线互相垂直的凸四边形叫做“垂直四边形”.
(1)理解:
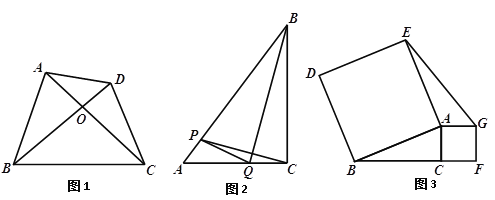
如图1,已知四边形ABCD是“垂直四边形”,对角线AC,BD交于点O,AC=8,BD=7,求四边形ABCD的面积.
(2)探究:
小明对 “垂直四边形”ABCD(如图1)进行了深入探究,发现其一组对边的平方和等于另一组对边的平方和.即![]() .你认为他的发现正确吗?试说明理由.
.你认为他的发现正确吗?试说明理由.
(3)应用:
① 如图2,在△ABC中, ![]() ,AC=6,BC=8,动点P从点A出发沿AB方向以每秒5个单位的速度向点B匀速运动,同时动点Q从点C出发沿CA方向以每秒6个单位的速度向点A匀速运动,运动时间为t秒(
,AC=6,BC=8,动点P从点A出发沿AB方向以每秒5个单位的速度向点B匀速运动,同时动点Q从点C出发沿CA方向以每秒6个单位的速度向点A匀速运动,运动时间为t秒(![]() ),连结CP,BQ,PQ.当四边形BCQP是“垂直四边形”时,求t的值.
),连结CP,BQ,PQ.当四边形BCQP是“垂直四边形”时,求t的值.
② 如图3,在△ABC中,![]() ,AB=3AC,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连结EG.请直接写出线段EG与BC之间的数量关系.
,AB=3AC,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连结EG.请直接写出线段EG与BC之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>x+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com