
【题目】如图,一次函数y=mx+n(m≠0)的图象与反比例函数y![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为点M,BM=OM=2,点A的纵坐标为4.
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为点M,BM=OM=2,点A的纵坐标为4.
(1)求该反比例函数和一次函数的表达式;
(2)根据图象直接写出当mx+n![]() 时,x的取值范围;
时,x的取值范围;
(3)直线AB交x轴于点D,过点D作直线l⊥x轴,如果直线l上存在点P,坐标平面内存在点Q,使以O、P、A、Q为顶点的四边形是矩形,直接写出点P的坐标.

【答案】(1)y![]() ,y=2x+2;(2)x>1或﹣2<x<0;(3)存在,点P的坐标为(﹣1,
,y=2x+2;(2)x>1或﹣2<x<0;(3)存在,点P的坐标为(﹣1,![]() )或(﹣1,
)或(﹣1,![]() )或(﹣1,2
)或(﹣1,2![]() )或(﹣1,2
)或(﹣1,2![]() ).
).
【解析】
(1)根据题意得出B点坐标,进而得出反比例函数解析式,再利用待定系数法得出一次函数解析式;
(2)若mx+n![]() ,结合图象可知即一次函数图象再反比例函数图象之上,结合图象即可求解;
,结合图象可知即一次函数图象再反比例函数图象之上,结合图象即可求解;
(3)若以O、P、A、Q为顶点的四边形是矩形,则存在两种情况,①若AO为边,②若AO是对角线.
(1)∵BM=OM=2,
∴点B的坐标为(﹣2,﹣2),
设反比例函数的解析式为y![]() ,
,
则﹣2![]() ,
,
得k=4,
∴反比例函数的解析式为y![]() ,
,
∵点A的纵坐标是4,
∴4![]() ,得x=1,
,得x=1,
∴点A的坐标为(1,4).
∵一次函数y=mx+n(m≠0)的图象过点A(1,4)、点B(﹣2,﹣2),
∴![]() ,
,
解得:![]() ,
,
即一次函数的解析式为y=2x+2;
(2)由图象可得当x>1或﹣2<x<0时,mx+n![]() ;
;
(3)存在,
若AO为边,
如图1,当四边形POAQ是矩形时,则∠POA=90°,
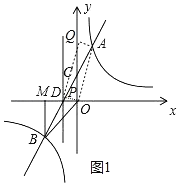
∵点A(1,4),点O(0,0),∴AO解析式为y=4x,∴直线DO解析式为:y![]() x.
x.
∵直线AB于x轴交于D,∴D(﹣1,0),∴OD=1,
设P(﹣1,a),∴a![]() ,∴点P(﹣1,
,∴点P(﹣1,![]() );
);
当四边形PAOQ是矩形,则∠PAO=90°,
同理可求:点P(﹣1,![]() );
);
若AO是对角线,
如图2,当∠APO=90°,
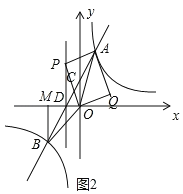
∵OP2=OA2﹣PA2=PD2+OD2,∴12+42﹣[(1+1)2+(4﹣a)2]=12+a2,
解得:a=2±![]() ,∴P(﹣1,2
,∴P(﹣1,2![]() )或(﹣1,2
)或(﹣1,2![]() ),
),
综上所述:点P的坐标为(﹣1,![]() )或(﹣1,
)或(﹣1,![]() )或(﹣1,2
)或(﹣1,2![]() )或(﹣1,2
)或(﹣1,2![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣mx+n经过点A(3,0).
(1)当m+n=﹣1时,求该抛物线的解析式和顶点坐标;
(2)当B点坐标为(0,﹣3)时,若抛物线y=x2﹣mx+n图象的顶点在直线AB上,求m、n的值;
(3)①设m=﹣2,当0≤x≤3时,求抛物线y=x2﹣mx+n的最小值;
②若当0≤x≤3时,二次函数y=x2﹣mx+n的最小值为﹣4,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
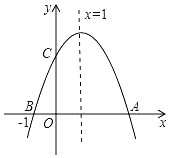
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:
①abc>0;②8a+c<0;③b2﹣4ac>0;④当y<0时,x<﹣1或x>2.
其中正确的有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…以此类推,则第2020个三角形的周长是_____.
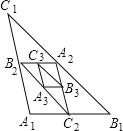
查看答案和解析>>
科目:初中数学 来源: 题型:
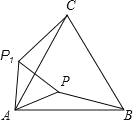
【题目】△ABC 是等边三角形,点 P 在△ABC 内,PA=2,将△PAB 绕点 A 逆时针旋转得到△P1AC,则 P1P 的长等于( )
A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com