
 有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=$\frac{1}{2}$,其中正确的有( )
有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=$\frac{1}{2}$,其中正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 ①根据旋转的性质,可得AM=MC=A′M=MC′=1,根据等腰三角形的性质,可得∠MCA′,根据等边三角形的判定,可得答案;
②根据垂线的性质:过直线外一点与已知直线垂直的直线只有一条,可得答案;
③根据等腰三角形的判定,可得答案
④根据平行四边形的判定,可得四边形AA′CC′是平行四边形,再根据有一个角是直角的平行四边形是矩形,可得答案;
⑤根据勾股定理可得BA的长,根据AB与AN的关系,可得AN的长,根据直角三角形的性质,可得答案.
解答 解:①∵点M是线段AC、线段A′C′的中点,AC=2,
∴AM=MC=A′M=MC′=1,
∵∠MA′C=30°,
∴∠MCA′=∠MA′C=30°,
∴∠A′MC=180°-30°-30°=120°,
∴∠A′MA=180°-A′MC=180°-120°=60°,
∴∠AMA′=∠C′MC=60°,
∴△AA′M是等边三角形,
∴AA′=AM=1,故①正确;
②∵∠A′CM=30°,∠MCC′=60°,
∴∠ACA′=∠A′CM+∠MCC′=90°,
∴CC′⊥A′C,故②正确;
③∵∠A′CA=∠NAC=30°,∠BCN=∠CBN=60°,
∴AN=NC=NB,故③正确;
④∵△AA′M≌△C′CM,
∴AA′=CC′,∠MAA′=∠C′CM=60°,
∴AA′∥CC′,
∴四边形AA′CC′是平行四边形,
∵∠AA′C=∠AA′M+∠MA′C=90°,
四边形AA′CC′为矩形,故④正确;
⑤AN=$\frac{1}{2}$AB=$\frac{2\sqrt{3}}{3}$,
∠NAA′=30°,∠AA′N=90°,
∴A′N=$\frac{1}{2}$AN=$\frac{\sqrt{3}}{3}$,故⑤错误;
故选:C.
点评 本题考查了旋转的性质,利用了旋转的性质,矩形的判定,等边三角形的判定,直角三角形的性质,所用知识点较多,题目稍有难度.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
 如图:O是正方形ABCD对角线的交点,圆心角为90°的扇形EOF从图1位置,顺时针旋转到图2位置,OE、OF分别交AD、AB于G、H.
如图:O是正方形ABCD对角线的交点,圆心角为90°的扇形EOF从图1位置,顺时针旋转到图2位置,OE、OF分别交AD、AB于G、H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
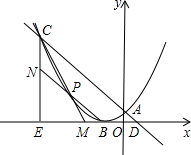 如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.
如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.在这个变化过程中,变量x表示点R运动的路程,变量y表示△MNR的面积,图2表示变量y随x的变化情况,则当y=9时,点R所在的边是:PN边或QM边.
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.在这个变化过程中,变量x表示点R运动的路程,变量y表示△MNR的面积,图2表示变量y随x的变化情况,则当y=9时,点R所在的边是:PN边或QM边.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
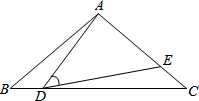 如图,在等腰△ABC中,AB=AC=9cm,BC=12cm,点D从B出发以每秒2cm的速度在线段BC上从B向C运动,点E同时从C出发以每秒2cm的速度在线段AC上从C向A运动,连接AD、DE.设运动时间为t秒,当∠ADE=90°-$\frac{1}{2}$∠BAC时,
如图,在等腰△ABC中,AB=AC=9cm,BC=12cm,点D从B出发以每秒2cm的速度在线段BC上从B向C运动,点E同时从C出发以每秒2cm的速度在线段AC上从C向A运动,连接AD、DE.设运动时间为t秒,当∠ADE=90°-$\frac{1}{2}$∠BAC时,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2013年8月由于持续高温和长时间无雨,南湖蓄水库的水量随着时间的增加而减少,干旱持续时间t天与蓄水量v(万立方米)的关系如图所示,回答下列问题:
2013年8月由于持续高温和长时间无雨,南湖蓄水库的水量随着时间的增加而减少,干旱持续时间t天与蓄水量v(万立方米)的关系如图所示,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )
如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com