
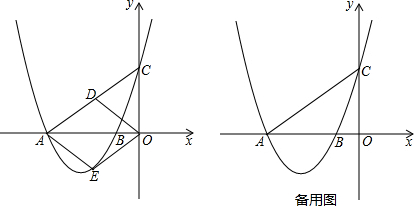
���� ��1�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ����x=0ʱ���ɵ�C�����꣬��y=0ʱ���ɵ�A��B�����ꣻ
��2�����ݴ���ϵ�������ɵ�AC�Ľ���ʽ�����ݺ�������ʽ���ɵ�D�����꣬����D��E����x��Գƣ��ɵ�E�����꣬����E���������������ϣ��ɵù���a�ķ��̣����ݽⷽ�̣��ɵ�D�����꣬���������߶���ȵ��ı��������Σ��ɵô𰸣�
��3���������������ε����ʣ��ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
��� �⣺��1����y=0ʱ��$\frac{3}{4}$x2+$\frac{15}{4}$x+3=0�����x1=-4��x2=-1����A��-4��0����B��-1��0����
��x=0ʱ��y=3����C��0��3����
��2����AC�Ľ���ʽΪy=kx+b����A��C������룬��
$\left\{\begin{array}{l}{-4k+b=0}\\{b=3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=3}\end{array}\right.$��
AC�Ľ���ʽΪy=$\frac{3}{4}$x+3��
��D��a��$\frac{3}{4}$a+3������D��E����x��Գƣ���E��a��-$\frac{3}{4}$a-3����
��E��������������ߣ���$\frac{3}{4}$a2+$\frac{15}{4}$a+3=-$\frac{3}{4}$a-3��
���a=-2��a=-4������������Ҫ��ȥ����
D��-2��$\frac{3}{2}$����
�ı���AEDO�����Σ��������£�
�ߡ�ADO���AEO����x��Գƣ�
��AD=AE��DO=EO��
��DE��AO�Ĵ�ֱƽ���ߣ�
��AD=DO��
��AD=AE=DO=EO��
���ı���AEDO�����Σ�
��3����ͼ��
��MNC�ס�AOCʱ��$\frac{MN}{AO}$=$\frac{CN}{CO}$��
��m��0ʱ��$\frac{m}{4}$=$\frac{\frac{3}{4}{m}^{2}+\frac{15}{4}m}{3}$��
���m=0������������Ҫ��ȥ����m=-12������������Ҫ��ȥ����
��-1��m��0ʱ��$\frac{m}{4}$=$\frac{-\frac{3}{4}{m}^{2}-\frac{15}{4}m}{3}$�����m=0������������Ҫ��ȥ��m=-6������������Ҫ��ȥ����
��-4��m��-1ʱ��$\frac{m}{4}$=$\frac{-\frac{3}{4}{m}^{2}-\frac{15}{4}m}{3}$�����m=0������������Ҫ��ȥ��m=-6������������Ҫ��ȥ����
��m��-4ʱ��$\frac{m}{4}$=$\frac{\frac{3}{4}{m}^{2}+\frac{15}{4}m}{3}$��
���m=0������������Ҫ��ȥ����m=-12��
����������m=-12ʱ����MNC�ס�AOC��
���� ���⿼���˶��κ����ۺ��⣬��1���������Ա����뺯��ֵ�Ķ�Ӧ��ϵ����2����������ԳƵ����ʣ����ε��ж�����3�����������������ε����ʣ����������ǽ���ؼ���


 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����ԭ��͵�A��2��0����������y=ax2+bx+c��˫����y=$\frac{k}{x}$����B��3��3����
����ԭ��͵�A��2��0����������y=ax2+bx+c��˫����y=$\frac{k}{x}$����B��3��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
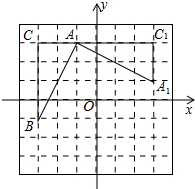 ��ͼ����ƽ��ֱ������ϵ�У���һRt��ABC����A��-1��3����B��-3��-1����C��-3��3������֪��A1AC1���ɡ�ABC��ת�õ��ģ�����ת���ĵ������ǣ�������
��ͼ����ƽ��ֱ������ϵ�У���һRt��ABC����A��-1��3����B��-3��-1����C��-3��3������֪��A1AC1���ɡ�ABC��ת�õ��ģ�����ת���ĵ������ǣ�������| A�� | ��0��0�� | B�� | ��-1��0�� | C�� | ��1��0�� | D�� | ��0��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
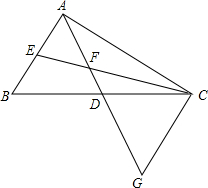 ��ͼ����ABC�У�D��E�ֱ�ΪBC��AB�е㣬����EC��AD����AD��EC���ڵ�F���ӳ�AD����GʹGD=AD������CG��
��ͼ����ABC�У�D��E�ֱ�ΪBC��AB�е㣬����EC��AD����AD��EC���ڵ�F���ӳ�AD����GʹGD=AD������CG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
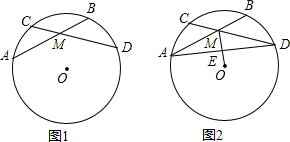
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
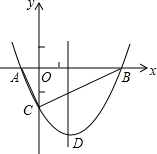 ��ͼ��������y=$\frac{1}{2}$x2+bx-2��x�ύ��A��B���㣬��y�ύ��C�㣬��A��һ1��0����
��ͼ��������y=$\frac{1}{2}$x2+bx-2��x�ύ��A��B���㣬��y�ύ��C�㣬��A��һ1��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
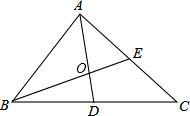 ��ͼ���ڡ�ABC�У�����AD��BE����O����S��BOD=5����S��BOA=10��
��ͼ���ڡ�ABC�У�����AD��BE����O����S��BOD=5����S��BOA=10���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
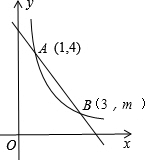 ��ͼ����ֱ������ϵxOy�У�һ�κ���y1=k1x+b��ͼ���뷴��������y2=$\frac{{k}_{2}}{x}$��ͼ����A��1��4����B��3��m�����㣮
��ͼ����ֱ������ϵxOy�У�һ�κ���y1=k1x+b��ͼ���뷴��������y2=$\frac{{k}_{2}}{x}$��ͼ����A��1��4����B��3��m�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���A=90�㣬��ABC��ƽ����BD��AC�ڵ�D��AD=2��BC=9�����BDC�������9��
��ͼ����Rt��ABC�У���A=90�㣬��ABC��ƽ����BD��AC�ڵ�D��AD=2��BC=9�����BDC�������9���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com