
【题目】某中学九年级的同学参加了一项“节能环保”的社会调查活动,为了了解家庭用电的情况,他们随机调查了某城区50 个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).

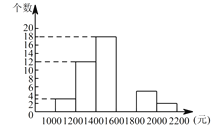
请你根据以上提供的信息,解答下列问题:
(1)频数分布表中 ![]() ________________,
________________,![]() ________________,
________________,
(2)补全频数分布直方图;
(3)这 ![]() 个家庭电费支出的中位数落在________组内;
个家庭电费支出的中位数落在________组内;
(4)若该城区有 ![]() 万个家庭,请你估计该城区有多少个一年电费支出低于
万个家庭,请你估计该城区有多少个一年电费支出低于 ![]() 元的家庭?
元的家庭?
【答案】(1)10;0.100;(2)补图见解析;(3)![]() ;(4)9000个.
;(4)9000个.
【解析】
(1)频数=频率×总数,由第1组可得到样本容量,再计算第四组的频数和第五组的频率;
(2)根据(1)的结果即可补全条形统计图;
(3)共有50个数,那么中位数就是按顺序排列后第25个和第26个的平均数;
(4)应先算出样本中电费支出低于1400元的家庭占50个家庭的百分比,乘以30000即可.
(1)样本容量=3÷0.060=50,第四组的频数=0.2×50=10;第五组的频率=5÷50=0.1;
故表中应填10和0.100.
(2)如图所示:
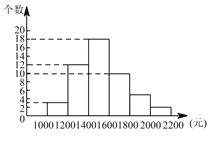
(3)总共有50个数据,中位数为第25个和第26个数的平均数,故中位数落在1400~1600这个组内.
(4)每年电费支出低于 ![]() 元的家庭数为
元的家庭数为 ![]() (个).
(个).
答:估计该地区有 ![]() 个一年电费支出低于
个一年电费支出低于 ![]() 元的家庭.
元的家庭.


科目:初中数学 来源: 题型:
【题目】观察下列各式:![]() ···①,
···①,![]() ···②,
···②,![]() …③,…
…③,…
探索以上式子的规律.
(1)第7个式子是_______;
(2)试写出第![]() 个等式,并说明第
个等式,并说明第![]() 个等式成立;
个等式成立;
(3)根据以上规律写出第2019个式子:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD为∠ABC的平分线,DE⊥BC于E,且AB+BC=2BE.
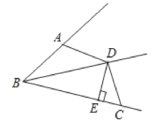
(1)求证:∠BAD+∠BCD=180°;
(2)若将条件“AB+BC=2BE”与结论“∠BAD+∠BCD=180°”互换,结论还成立吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
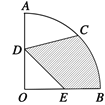
【题目】如图,在圆心角为 ![]() 的扇形
的扇形 ![]() 中,半径
中,半径 ![]() =4cm,
=4cm,![]() 为弧
为弧 ![]() 的中点,
的中点,![]() ,
,![]() 分别是
分别是 ![]() ,
,![]() 的中点,则图中阴影部分的面积(单位
的中点,则图中阴影部分的面积(单位![]() )为( )
)为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为5,弦AB⊥CD于E,AB=CD=8.
(1)求证:AC=BD;
(2)若OF⊥CD于F,OG⊥AB于G,试说明四边形OFEG是正方形;
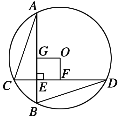
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,其中
,其中![]() .
.
(1)若点![]() 在y1的图象上.求a的值:
在y1的图象上.求a的值:
(2)当![]() 时.若函数有最大值2.求y1的函数表达式;
时.若函数有最大值2.求y1的函数表达式;
(3)对于一次函数![]() ,其中
,其中![]() ,若对- -切实数x,
,若对- -切实数x,![]() 都成立,求a,m需满足的数量关系及 a的取值范围.
都成立,求a,m需满足的数量关系及 a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com