
| |||||||||||||||
(1) |
证明:∵∠DEF=45°,得∠DFE=90°-∠DEF=45°,∴∠DFE=∠DEF,∴DE=DF,又∵AD=DC,∴AE=FC.因为AB是圆B的半径,AD⊥AB,所以AD切圆B于点A;同理,CD切圆B于点C,又因为EF切圆B于点G,所以AE=EG,FC=FG,因此EG=FG,即点G为线段EF的中点. |
(2) |
解:∵EG=AE=x,FG=CF=y,∴ED=1-x,FD=1-y,在Rt△DEF中,由ED2+FD2=EF2,得(1-x)2+(1-y)2=(x+y)2,∴y= |
(3) |
解:当EF=
|


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:
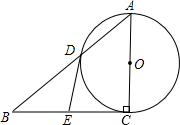 ,交BC于点E.
,交BC于点E.| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
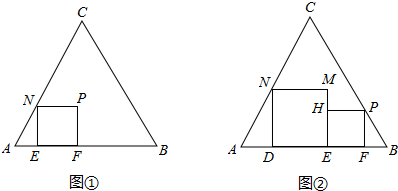
查看答案和解析>>
科目:初中数学 来源: 题型:
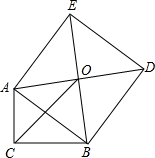 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com