
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
分析 先根据题意设出A、B两点的坐标,进而可得出结论.
解答 解:∵点A、B分别是函数y=$\frac{4}{x}$(x>0)和y=-$\frac{4}{x}$(x<0)图象上的一点,A、B两点的横坐标分别为a、b,
∴A(a,$\frac{4}{a}$),B(b,-$\frac{4}{b}$)且a>0,b<0.
∵OA=OB,a+b≠0,
∴a=-$\frac{4}{b}$,b=-$\frac{4}{a}$,
∴ab=$\frac{4}{b}$•$\frac{4}{a}$=$\frac{16}{ab}$,
∴ab=-4.
故选D.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


科目:初中数学 来源: 题型:选择题
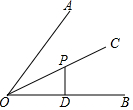 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
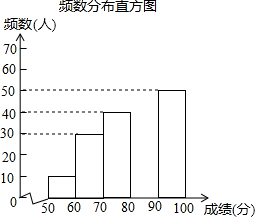 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:| 成绩x(分) | 频数(人) | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 40 | n |
| 80≤x<90 | m | 0.35 |
| 90≤x≤100 | 50 | 0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (4,$\frac{17}{6}$) | B. | (4,3) | C. | (5,$\frac{17}{6}$) | D. | (5,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
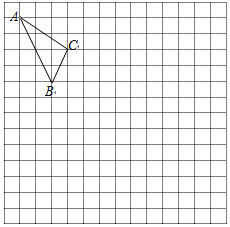 在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4).
在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4).查看答案和解析>>
科目:初中数学 来源:2016-2017学年山东省新泰市六年级(五四学制)下学期第一次月考数学试卷(解析版) 题型:填空题
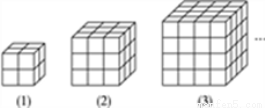
如图,下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),则第n个几何体中只有两个面涂色的小立方体共有__________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com