
如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
某城市的A商场和B商场都卖同一种电动玩具,A商场的单价与B商场的单价之比是 5:4,用120元在A商场买这种电动玩具比在B商场少买2个,求这种电动玩具在A商场和B商场的单价.
5:4,用120元在A商场买这种电动玩具比在B商场少买2个,求这种电动玩具在A商场和B商场的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
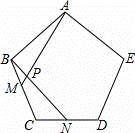
如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点 P、Q移动的时间为t秒.
P、Q移动的时间为t秒.
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为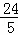 个平方单位?
个平方单位?

查看答案和解析>>
科目:初中数学 来源: 题型:
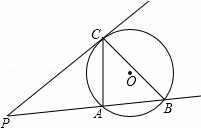
已知:如图,P是⊙O外一点,过点P引圆的切线PC(C为切点)和割线PAB,分别交⊙O于A、B,连接AC,BC.
(1)求证:∠PCA=∠PBC;
(2)利用(1)的结论,已知PA=3,PB=5,求PC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com