
分析 首先根据题意画出图形,理由符号表示出已知条件,然后再根据等边三角形的性质可得AB=AC=BC,∠BAC=∠ABC=∠ACB=60°,再利用三线合一的性质和全等三角形的判定方法证明全等三角形即可.
解答 已知:△ABC是等边三角形,CE、BF、AD是三条中线,交于点O,
找出图中所有的全等三角形,并证明.
证明:∵△ABC是等边三角形,
∴AB=AC,
∵AD是中线,
∴BD=CD,
在△ABD和△ACD中$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ACD(SSS),
同理:△ABF≌△BCF,△ACE≌△BCE,
∵AC=AB,CE、BF是中线,
∴AE=AF,
∵在△ABF和△ACE中$\left\{\begin{array}{l}{AB=AC}\\{∠BAF=∠CAE}\\{AF=AE}\end{array}\right.$,
∴△ACE≌△ABF(SAS);
同理:△ADC≌△BFC,△ABD≌△CBE,
∴△ABD≌△ACD≌△CBE≌△BFC≌△BFA≌△CEA;
∵△ABC是等边三角形,AD是中线,
∴∠BAO=∠CAO,
在△AEO和△AFO中$\left\{\begin{array}{l}{AE=AF}\\{∠EAO=∠FAO}\\{AO=AO}\end{array}\right.$,
∴△AEO≌△AFO(SAS),
∵△ABC是等边三角形,AD是中线,
∴∠AEO=∠BEO=90°,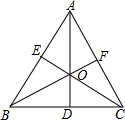
在△AEO和△BEO中$\left\{\begin{array}{l}{AE=BE}\\{∠AEO=∠BEO}\\{EO=EO}\end{array}\right.$,
∴△AEO≌△BEO(SAS),
∴△AEO≌△AFO≌△BEO,
同理:△BEO≌△BDO≌△CDO≌△CFO≌△AFO,
∴△AEO≌△AFO≌△BEO≌△BDO≌△CDO≌△CFO;
在△ABO和△ACO中$\left\{\begin{array}{l}{AB=AC}\\{∠BAO=∠CAO}\\{AO=AO}\end{array}\right.$,
∴△ABO≌△ACO(SAS),
同理△CBO≌△CAO,
∴△ABO≌△ACO≌△BCO.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
 某城区规划局为了方便居民的生活,计划在三个住宅小区A,B,C(如图所示) 之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场距离相等?
某城区规划局为了方便居民的生活,计划在三个住宅小区A,B,C(如图所示) 之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场距离相等?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
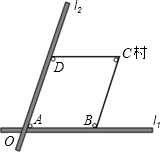 如图,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D.已知AB=BC=CD=DA=5公里,村庄C到公路l1的距离为4公里,则村庄C到公路l2的距离是( )
如图,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D.已知AB=BC=CD=DA=5公里,村庄C到公路l1的距离为4公里,则村庄C到公路l2的距离是( )| A. | 3km | B. | 4km | C. | 5km | D. | 6km |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
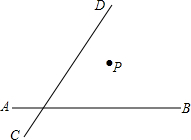 如图所示,P为马厩,AB为草地边缘(下方为草地),CD为一河流,牧人欲从马厩牵马先去草地吃草,然后到河边饮水,最后回到马厩,请帮他确定一条最佳行走路线.
如图所示,P为马厩,AB为草地边缘(下方为草地),CD为一河流,牧人欲从马厩牵马先去草地吃草,然后到河边饮水,最后回到马厩,请帮他确定一条最佳行走路线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com