练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知（m﹣n）2=34，（m+n）2=4 000，则m2+n2的值为（ ）
    A.2 016
    B.2 017
    C.2 018
    D.4 034

    【答案】B
    【解析】解：∵（m﹣n）2=m2﹣2mn+n2=34①，（m+n）2=m2+2mn+n2=4000②， ∴①+②得：2（m2+n2）=4034，
    则m2+n2=2017，
    故选B
    【考点精析】利用完全平方公式对题目进行判断即可得到答案，需要熟知首平方又末平方，二倍首末在中央．和的平方加再加，先减后加差平方．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】正五边形的外角和为（ ）

    A. 180°B. 540°C. 360°D. 72°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

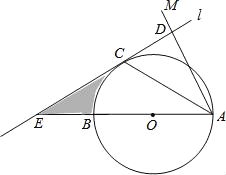
    【题目】如图，AB为⊙O的直径，点C为⊙O上一点，若∠BAC=∠CAM，过点C作直线l垂直于射线AM，垂足为点D．

    （1）试判断CD与⊙O的位置关系，并说明理由；

    （2）若直线l与AB的延长线相交于点E，⊙O的半径为3，并且∠CAB=30°．求图中所示阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点A（﹣4，﹣3）在（ ）

    A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：

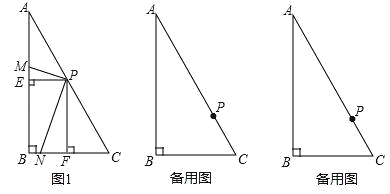
    【题目】已知：在Rt△ABC中，∠ABC=90°，∠C=60°，现将一个足够大的直角三角形的顶点P放在斜边AC上．

    （1）设三角板的两直角边分别交边AB，BC于点M，N．

    ①当点P是AC的中点时，分别作PE⊥AB于点E，PF⊥BC于点F，得到图1，写出图中的一对全等三角形；

    ②在①的条件下，写出与△PEM相似的三角形，并直接写出PN与PM的数量关系．

    （2）移动点P，使AP=2CP，将三角板绕点P旋转，设旋转过程中三角板的两直角边分别交边AB，BC于点M，N（PM不与边AB垂直，PN不与边BC垂直）；或者三角板的两直角边分别交边AB，BC的延长线于点M，N．

    ①请在备用图中画出图形，判断PM与PN的数量关系，并选择其中一种图形证明你的结论；

    ②在①的条件下，当△PCN是等腰三角形时，若BC=3cm，则线段BN的长是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：x2y﹣2xy2+y3= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下面推理过程：

    已知：如图，已知∠1 ＝∠2，∠B ＝∠C，

    求证：AB∥CD．

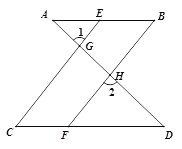
    证明∵∠1 ＝∠2（已知），

    且∠1 ＝∠CGD（ ），

    ∴∠2 ＝∠CGD（等量代换）．

    ∴CE∥BF（ ）．

    ∴∠ ＝∠C（ ）．

    又∵∠B ＝∠C（已知），

    ∴∠ ＝∠B（等量代换）．

    ∴AB∥CD（ ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从分别标有1，2，3，…，50的50张卡片中抽出2的倍数的卡片的可能性________抽出4的倍数的卡片的可能性(填“大于”“小于”或“等于”)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙、丙、丁四位同学五次100米跑成绩统计如下表.如果从这四位同学中，选出一位成绩较好且状态稳定的同学参加县运动会，那么应选（ ）

    甲

    乙

    丙

    丁

    平均数（秒）

    16

    15

    15

    16

    方差

    30

    30

    35

    42

    A. 甲B. 乙C. 丙D. 丁

    查看答案和解析>>

    同步练习册答案