练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（ ）
    A.
    B.2
    C.
    D.

    【答案】B
    【解析】解：∵∠ABC=90°， ∴∠ABP+∠PBC=90°，
    ∵∠PAB=∠PBC，
    ∴∠BAP+∠ABP=90°，
    ∴∠APB=90°，
    ∴OP=OA=OB（直角三角形斜边中线等于斜边一半），
    ∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，此时PC最小，
    在RT△BCO中，∵∠OBC=90°，BC=4，OB=3，
    ∴OC= =5，
    ∴PC=OC﹣OP=5﹣3=2．
    ∴PC最小值为2．
    故选B．

    首先证明点P在以AB为直径的⊙O上，连接OC与⊙O交于点P，此时PC最小，利用勾股定理求出OC即可解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知矩形OABC的顶点A在x轴上，OA=4，OC=3，点D为BC边上一点，以AD为一边在与点B的同侧作正方形ADEF，连接OE．当点D在边BC上运动时，OE的长度的最小值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，CE垂直对角线AC于点C，AB的延长线交CE于点E．
    （1）求证：CD=BE；
    （2）如果∠E=60°，CE=m，请写出求菱形ABCD面积的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系；

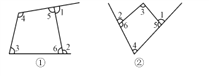
    (2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;

    (3)用你发现的结论解决下列问题:

    如图,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC的底边BC=10cm，当BC边上的高线AD从小到大变化时，△ABC的面积也随之变化．

    （1）在这个变化过程中，自变量和因变量各是什么？

    （2）△ABC的面积S（cm2）与高线h（cm）之间的关系式是什么？

    （3）用表格表示当h由4cm变到10cm时（每次增加1cm），S的相应值；

    （4）当h每增加1cm时，S如何变化？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2018年1月20日，山西迎来了“复兴号”列车，与“和谐号”相比，“复兴号”列车时速更快，安全性更好．已知“太原南﹣北京西”全程大约500千米，“复兴号”G92次列车平均每小时比某列“和谐号”列车多行驶40千米，其行驶时间是该列“和谐号”列车行驶时间的（两列车中途停留时间均除外）．经查询，“复兴号”G92次列车从太原南到北京西，中途只有石家庄一站，停留10分钟．求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△BCE中，点A是边BE上一点，以AB为直径的⊙O与CE相切于点D，AD∥OC，点F为OC与⊙O的交点，连接AF．
    （1）求证：CB是⊙O的切线；
    （2）若∠ECB=60°，AB=6，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一单杆高2.2m，两立柱之间的距离为1.6m，将一根绳子的两端栓于立柱与铁杠结合处，绳子自然下垂呈抛物线状．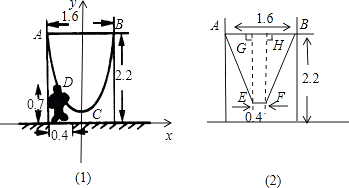
    （1）一身高0.7m的小孩站在离立柱0.4m处，其头部刚好触上绳子，求绳子最低点到地面的距离；
    （2）为供孩子们打秋千，把绳子剪断后，中间系上一块长为0.4米的木板，除掉系木板用去的绳子后，两边的绳子正好各为2米，木板与地面平行，求这时木板到地面的距离．（供选用数据： ≈1.8， ≈1.9， ≈2.1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰△ABC中，∠A=36°，∠ABC=∠ACB，∠1=∠2，∠3=∠4，BD与CE交于点O，则图中等腰三角形有（　　）

    A. 6个 B. 7个 C. 8个 D. 9个

    查看答案和解析>>

    同步练习册答案