
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2ax+2
(1)求抛物线的对称轴(用含a的代数式表示)
(2)若点A(﹣1,3)向右平移4个长度单位,得到点B.
①若抛物线经过点B,求a的值;
②抛物线与线段AB恰有一个交点,结合函数图象,直接写出a的取值范围.
【答案】(1)抛物线的对称轴为直线x=a;(2)a=±1或a>![]() 时,抛物线与线段AB有一个公共点.
时,抛物线与线段AB有一个公共点.
【解析】
(1)利用抛物线的对称轴公式:![]() 求解即可;(2)利用平移规律写出点B的坐标;①将点B的坐标代入解析式求解;②求顶点的坐标可知,抛物线的顶点在抛物线y=x2+2上移动,求得抛物线与直线y=3的交点.再求出抛物线过点A、点B时,a的值,结合图象即可求出a的取值范围.
求解即可;(2)利用平移规律写出点B的坐标;①将点B的坐标代入解析式求解;②求顶点的坐标可知,抛物线的顶点在抛物线y=x2+2上移动,求得抛物线与直线y=3的交点.再求出抛物线过点A、点B时,a的值,结合图象即可求出a的取值范围.
(1)∵抛物线y=﹣x2+2ax+2,
∴抛物线的对称轴为直线x=![]() ;
;
(2)点A(﹣1,3)向右平移4个长度单位,得到点B(3,3),
①∵抛物线经过点B,
∴3=﹣9+6a+2,
解得a=![]() ;
;
②∵y=﹣x2+2ax+2=﹣(x﹣a)2+a2+2,
∴顶点的坐标为(a,a2+2),
由顶点的坐标可知,抛物线的顶点在y=x2+2上移动.
把y=3代入y=x2+2求得x=±1,
当抛物线过点A(﹣1,3)时,a=﹣1.
所以a=±1或a>![]() 时,抛物线与线段AB有一个公共点.
时,抛物线与线段AB有一个公共点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() ,
,![]() 两点,其中点
两点,其中点![]() ,
,![]() ,点
,点![]() 都在抛物线上,
都在抛物线上,![]() 为抛物线的顶点.
为抛物线的顶点.
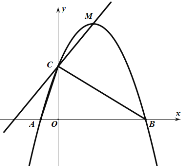
(1)求抛物线的函数解析式;
(2)求直线![]() 的解析式;
的解析式;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且经
,且经![]() 、
、![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴
在抛物线的对称轴![]() 上,是否存在点
上,是否存在点![]() ,使它到点
,使它到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,如果存在求出点
的距离之和最小,如果存在求出点![]() 的坐标,如果不存在请说明理由.
的坐标,如果不存在请说明理由.
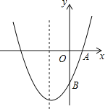
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有(除颜色外)完全相同的红色小球1个,白色小球1个和黄色小球2个,
(1)从中先摸出一个小球,记录下它的颜色后,将它放回袋中搅匀,再摸出一个小球,记录下颜色. 求摸出的两个小球的颜色恰好是“一红一黄”的概率是多少?
(2)如果摸出第一个小球之后不放回袋中,再摸出第二个小球,这时摸出的两个小球的颜色恰好是“一红一黄”的概率是多少?
(3)小明想给袋中加入一些红色的小球,使从袋中任意摸出一个小球恰为红色的概率为![]() ,请你帮小明算一算,应该加入多少个红色的小球?
,请你帮小明算一算,应该加入多少个红色的小球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,每人射击10次,成绩分别如下:
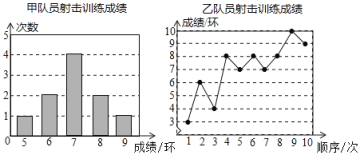
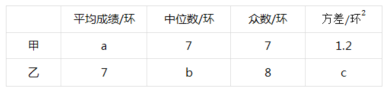
根据以上信息,整理分析数据如下:
(1)填空:a= ;b= ;c= ;
(2)从平均数和中位数的角度来比较,成绩较好的是 ;(填“甲”或“乙”)
(3)若需从甲、乙两名队员中选择一人参加比赛,你认为选谁更加合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
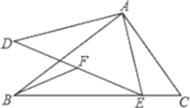
【题目】如图,△ABC∽△ADE,∠BAC=∠DAE=90°,AB=16,AC=12,F是DE的中点, 若点E是直线BC上的动点,连接BF,则BF的最小值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

(1)证明:DF是⊙O的切线;
(2)若AC=3AE,FC=6,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com