
【题目】矩形ABCD中,AB=2,AD=3,O为边AD上一点,以O为圆心,OA为半径r作⊙O,过点B作⊙O的切线BF,F为切点.
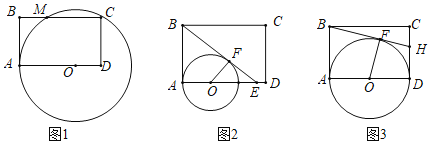
(1)如图1,当⊙O经过点C时,求⊙O截边BC所得弦MC的长度;
(2)如图2,切线BF与边AD相交于点E,当FE=FO时,求r的值;
(3)如图3,当⊙O与边CD相切时,切线BF与边CD相交于点H,设△BCH、四边形HFOD、四边形FOAB的面积分别为S1、S2、S3,求![]() 的值.
的值.
【答案】(1)CM=![]() ;(2)r=2
;(2)r=2![]() ﹣2;(3)1.
﹣2;(3)1.
【解析】
(1)如图1中,连接OM,OC,作OH⊥BC于H.首先证明CM=2OD,设AO=CO=r,在Rt△CDO中,根据OC2=CD2+OD2,构建方程求出r即可解决问题.
(2)证明△OEF,△ABE都是等腰直角三角形,设OA=OF=EF=r,则OE=![]() r,根据AE=2,构建方程即可解决问题.
r,根据AE=2,构建方程即可解决问题.
(3)分别求出S1、S2、S3的值即可解决问题.
解:(1)如图1中,连接OM,OC,作OH⊥BC于H.
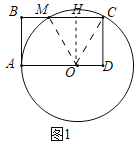
∵OH⊥CM,
∴MH=CH,∠OHC=90°,
∵四边形ABCD是矩形,
∴∠D=∠HCD=90°,
∴四边形CDOH是矩形,
∴CH=OD,CM=2OD,
设AO=CO=r,
在Rt△CDO中,∵OC2=CD2+OD2,
∴r2=22+(3﹣r)2,
∴r=![]() ,
,
∴OD=3﹣r=![]() ,
,
∴CM=2OD=![]() .
.
(2)如图2中,
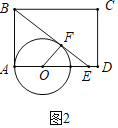
∵BE是⊙O的切线,
∴OF⊥BE,
∵EF=FO,
∴∠FEO=45°,
∵∠BAE=90°,
∴∠ABE=∠AEB=45°,
∴AB=BE=2,
设OA=OF=EF=r,则OE=![]() r,
r,
∴r+![]() r=2,
r=2,
∴r=2![]() ﹣2.
﹣2.
(3)如图3中,
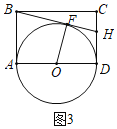
由题意:直线AB,直线BH,直线CD都是⊙O的切线,
∴BA=BF=2,FH=HD,设FH=HD=x,
在Rt△BCH中,∵BH2=BC2+CH2,
∴(2+x)2=32+(2﹣x)2,
∴x=![]() ,
,
∴CH=![]() ,
,
∴S1=![]()
S2=![]() ,
,
S3=![]() =3,
=3,
∴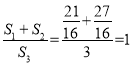 .
.


科目:初中数学 来源: 题型:
【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.

甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,
查看答案和解析>>
科目:初中数学 来源: 题型:
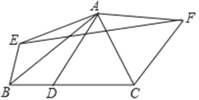
【题目】如图,△ABC中,∠BAC=75°,BC=7,△ABC的面积为14,D为 BC边上一动点(不与B,C重合),将△ABD和△ACD分别沿直线AB,AC翻折得到△ABE与△ACF,那么△AEF的面积最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
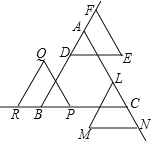
【题目】如图,等边△ABC的边长为5,点D,P,L分别在边AB,BC,CA上,AD=BP=CL=x(x>0).按如图方式作边长均为3的等边△DEF,△PQR,△LMN,点F,R,N分别在射线DA,PB,LC上.
①当边DE,PQ,LM与△ABC的三边围成的图形是正六边形时,x=_____;
②当点D与点B重合时,EF,QR,MN所围成的三角形的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
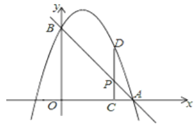
【题目】如图,已知抛物线![]() 分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若![]() .
.
①求抛物线的解析式;
②当线段PD的长度最大时,求点P的坐标;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
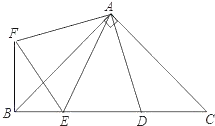
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,∠EAD=45°,将△ADC绕点A顺时针旋转90°,得到△AFB,连接EF.
(1)求证:EF=ED;
(2)若AB=2![]() ,CD=1,求FE的长.
,CD=1,求FE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
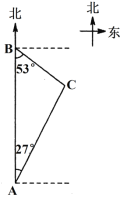
【题目】如图,海上有A、B、C三座小岛,小岛B在岛A的正北方向,距离为121海里,小岛C分别位于岛B的南偏东53°方向,位于岛A的北偏东27°方向,求小岛B和小岛C之间的距离.(参考数据:sin27°≈![]() ,cos27°≈
,cos27°≈![]() ,tan27°≈
,tan27°≈![]() ,sin53°≈
,sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
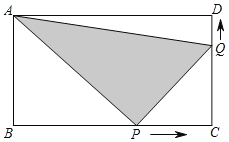
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点B出发沿线段BC、CD以2cm/s的速度向终点D运动;同时,点Q从点C出发沿线段CD、DA以1cm/s的速度向终点A运动(P、Q两点中,只要有一点到达终点,则另一点运动立即停止).
(1)运动停止后,哪一点先到终点?另一点离终点还有多远?
(2)在运动过程中,△APQ的面积能否等于22cm2?若能,需运动多长时间?若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com