练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图AB是⊙O的切线，切点为B，AO交⊙O于点C，过点C作DC⊥OA，交AB于点D.

    (1)求证：∠CDO＝∠BDO；

    (2)若∠A＝30°，⊙O的半径为4，求阴影部分的面积(结果保留π)．

    【答案】（1）见解析 （2）－

    【解析】

    (1)证明：AB切⊙O于点B，

    ∴OB⊥AB，即∠B＝90°.

    又∴DC⊥OA，∴∠OCD＝90°.

    在Rt△COD与Rt△BOD中，OD＝OD，OB＝OC，

    ∴Rt△COD≌Rt△BOD.

    ∴∠CDO＝∠BDO.

    (2)在Rt△ABO中，∠A＝30°，OB＝4，

    ∴∠BOC＝60°，

    ∵Rt△COD≌Rt△BOD，

    ∴∠BOD＝30°，

    ∴BD＝OB·tan 30°＝.

    ∴S四边形OCDB＝2S△OBD＝2××4×＝.

    ∵∠BOC＝60°，

    ∴S扇形OBC＝＝.

    ∴S阴影＝S四边形OCDB－S扇形OBC＝－.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点在反比例函数的图象上，点在反比例函数的图象上，且．线段交反比例函数的图象于另一点，连接OC，若点为的中点，则的值为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：二次函数，下列说法错误的是( )

    A. 当时，随的增大而减小

    B. 若图象与轴有交点，则

    C. 当时，不等式的解集是

    D. 若将图象向上平移个单位，再向左平移个单位后过点，则

    查看答案和解析>>

    科目：初中数学 来源： 题型：

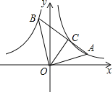
    【题目】如图，点A在抛物线y＝x2﹣2x+2上运动，过点A作AC上x轴于点C，以AC为对角线作矩形ABCD，连结BD，则BD的最小值为（　　）

    A. B. 1 C. D. 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

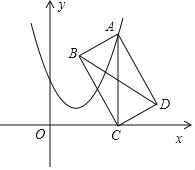
    【题目】如图，正六边形ABCDEF中，P、Q两点分别为△ACF、△CEF的内心．若AF=2，则PQ的长度为何？（　　）

    A. 1 B. 2 C. 2﹣2 D. 4﹣2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料，解答问题：

    （1）中国古代数学著作《周髀算经》有着这样的记载：“勾广三，股修四，经隅五．”这句话的意思是：“如果直角三角形两直角边为3和4时，那么斜边的长为5．”上述记载说明：在中，如果，，，，那么三者之间的数量关系是： ．

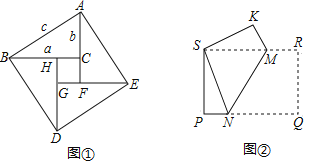
    （2）对于（1）中这个数量关系，我们给出下面的证明．如图①，它是由四个全等的直角三角形围成的一个大正方形，中空的部分是一个小正方形．结合图①，将下面的证明过程补充完整：

    ∵，

    （用含的式子表示）

    又∵ ．

    ∴

    ∴

    ∴ ．

    （3）如图②，把矩形折叠，使点与点重合，点落在点处，折痕为．如果，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

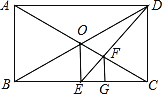
    【题目】如图所示，在矩形ABCD中，AC、BD相交于点O，OE⊥BC于E，连接DE交OC于点F，作FG⊥BC于G．

    (1)说明点G是线段BC的一个三等分点；

    (2)请你依照上面的画法，在原图上画出BC的一个四等分点（保留作图痕迹，不必证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

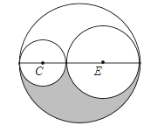
    【题目】如图所示，两个小圆的半径分别是2厘米和3厘米，最外侧大圆的面积是半径为2厘米的小圆面积的几倍？阴影部分的面积是半径为3厘米的圆的面积的多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

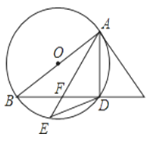
    【题目】如图，AB是⊙O的直径，AC是⊙O的切线，BC与⊙O相交于点D，点E在⊙O上，且DE=DA，AE与BC相交于点F．

    （1）求证：FD=DC；

    （2）若AE=8，DE=5，求⊙O的半径．

    查看答案和解析>>

    同步练习册答案