
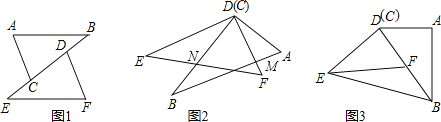
”¾ĢāÄæ”æČēĶ¼1ĖłŹ¾£¬ŅŃÖŖŌŚ”÷ABCŗĶ”÷DEFÖŠ£¬AB=EF£¬”ĻB=”ĻE£¬EC=BD
£Ø1£©ŹŌĖµĆ÷£ŗ”÷ABC”Õ”÷FED£»
£Ø2£©ČōĶ¼ŠĪ¾¹żĘ½ŅĘŗĶŠż×ŖŗóµĆµ½Ķ¼2£¬ĒŅÓŠ”ĻEDB=25”ć£¬”ĻA=66”ć£¬ŹŌĒó”ĻAMDµÄ¶ČŹż£»
£Ø3£©½«Ķ¼ŠĪ¼ĢŠųŠż×ŖŗóµĆµ½Ķ¼3£¬“ĖŹ±D£¬B£¬FČżµćŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬ČōDB=2DF£¬Į¬½ÓEB£¬ŅŃÖŖ”÷EFBµÄĆ껿ĪŖ5cm2£¬ÄćÄÜĒó³öĖıߊĪABEDµÄĆ껿Āš£æČōÄÜ£¬ĒėĒó³öĄ“£»Čō²»ÄÜ£¬ĒėÄćĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ¼ū½āĪö
”¾½āĪö”æ
ŹŌĢā£Ø1£©ÓÉEC=BD£¬µČŹ½×óÓŅĮ½±ß¶¼¼ÓÉĻDC£¬µĆµ½ED=BC£¬ŌŁÓÉ”ĻB=”ĻE£¬AB=EF£¬ĄūÓĆSASæÉÖ¤Ć÷Čż½ĒŠĪABCÓėČż½ĒŠĪFEDČ«µČ£»
£Ø2£©ÓÉČż½ĒŠĪABCÓėČż½ĒŠĪFEDČ«µČ£¬øł¾ŻČ«µČČż½ĒŠĪµÄ¶ŌÓ¦½ĒĻąµČ£¬µĆµ½”ĻEDF=”ĻBDA£¬µČŗÅĮ½±ß¶¼¼õČ„”ĻBDF£¬µĆµ½”ĻEDB=”ĻADF£¬ÓÉ”ĻEDBµÄ¶ČŹżµĆµ½”ĻADFµÄ¶ČŹż£¬ŌŚČż½ĒŠĪAMDÖŠ£¬ÓÉ”ĻADF¼°”ĻAµÄ¶ČŹż£¬ĄūÓĆČż½ĒŠĪµÄÄŚ½ĒŗĶ¶ØĄķ¼“æÉĒó³ö”ĻAMDµÄ¶ČŹż£»
£Ø3£©ÓÉBD=2DF£¬µĆµ½ĪŖDBµÄÖŠµć£¬æɵĆDF=BF£¬ĄūÓƵȵ×Ķ¬øßæɵĆČż½ĒŠĪDEFÓėČż½ĒŠĪEFBĆ껿ĻąµČ£¬ÓÖČż½ĒŠĪABDÓėČż½ĒŠĪDEFČ«µČ£¬µĆµ½Čż½ĒŠĪABDÓėČż½ĒŠĪDEFĆ껿ĻąµČ£¬æɵĆČż½ĒŠĪDEF£¬Čż½ĒŠĪEFBÓėČż½ĒŠĪABDµÄĆ껿¶¼ĻąµČ£¬ÓÉČż½ĒŠĪEFBµÄĆ껿æÉµĆ³öĘäĖüĮ½Čż½ĒŠĪµÄĆ껿£¬ČżÕßĻą¼ÓæÉµĆ³öĖıߊĪABEDµÄĆ껿£®
ŹŌĢā½āĪö£ŗ£Ø1£©”ßEC=BD£ØŅŃÖŖ£©£¬
”ąEC+CD=BD+DC£¬¼“ED=BC£¬
ŌŚ”÷ABCŗĶ”÷FEDÖŠ£¬
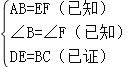 £¬
£¬
”ą”÷ABC”Õ”÷FED£ØSAS£©£»
£Ø2£©”ß”÷ABC”Õ”÷FED£¬
”ą”ĻEDF=”ĻBDA£¬
”ą”ĻEDF©”ĻBDF=”ĻBDA©”ĻBDF£¬ÓÖ”ĻEDB=25”ć£¬
”ą”ĻEDB=”ĻADF=25”ć£¬ÓÖ”ĻA=66”ć£¬
”ą”ĻAMD=180”ć©66”ć©25”ć=89”ć£»
£Ø3£©ÄÜĒó³öĖıߊĪABEDµÄĆ껿£¬·½·ØĪŖ£ŗ
”ß”÷ABC”Õ”÷FED£¬
”ąS”÷ABC=S”÷FED£¬
”ßDB=2DF£¬¼“FĪŖBDÖŠµć£¬
”ąDF=BF£¬ÓÖS”÷EFB=5£¬
”ąS”÷EDF=S”÷EFB=S”÷ABC=5£¬
”ąSABCD=S”÷EDF+S”÷EFB+S”÷ABC=15£®


 ÖĒÄÜѵĮ·Į·²āæ¼ĻµĮŠ“š°ø
ÖĒÄÜѵĮ·Į·²āæ¼ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬DŹĒBC±ßÉĻµÄµć£Ø²»ÓėµćB”¢CÖŲŗĻ£©£¬Į¬½įAD£®
ĪŹĢāŅżČė£ŗ
£Ø1£©ČēĶ¼¢Ł£¬µ±µćDŹĒBC±ßÉĻµÄÖŠµćŹ±£¬S”÷ABD£ŗS”÷ABC=£»µ±µćDŹĒBC±ßÉĻČĪŅāŅ»µćŹ±£¬S”÷ABD£ŗS”÷ABC=£ØÓĆĶ¼ÖŠŅŃÓŠĻ߶Ī±ķŹ¾£©£®
£Ø2£©ČēĶ¼¢Ś£¬ŌŚ”÷ABCÖŠ£¬OµćŹĒĻ߶ĪADÉĻŅ»µć£Ø²»ÓėµćA”¢DÖŲŗĻ£©£¬Į¬½įBO”¢CO£¬ŹŌ²ĀĻėS”÷BOCÓėS”÷ABCÖ®±ČÓ¦øƵČÓŚĶ¼ÖŠÄÄĮ½ĢõĻ߶ĪÖ®±Č£¬²¢ĖµĆ÷ĄķÓÉ£®
£Ø3£©ČēĶ¼¢Ū£¬OŹĒĻ߶ĪADÉĻŅ»µć£Ø²»ÓėµćA”¢DÖŲŗĻ£©£¬Į¬½įBO²¢ŃÓ³¤½»ACÓŚµćF£¬Į¬½įCO²¢ŃÓ³¤½»ABÓŚµćE£¬ŹŌ²ĀĻė ![]() +
+ ![]() +
+ ![]() µÄÖµ£¬²¢ĖµĆ÷ĄķÓÉ£®
µÄÖµ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻB£½70”ć£¬”ĻBAC”Ć”ĻBCA£½3”Ć2£¬CD”ĶADÓŚµćD£¬µćE£¬A£¬DŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬ĒŅ”ĻACD£½35”ć£¬Ēó”ĻBAEµÄ¶ČŹż£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ±ß³¤ĪŖ1µÄŠ”Õż·½ŠĪ×é³ÉµÄ·½øńÖ½ÖŠ£¬³ĘŠ”Õż·½ŠĪµÄ¶„µćĪŖ”°øńµć”±£¬¶„µćČ«ŌŚøńµćÉĻµÄ¶ą±ßŠĪĪŖ”°øńµć¶ą±ßŠĪ”±£®øńµć¶ą±ßŠĪµÄĆ껿¼ĒĪŖS£¬ĘäÄŚ²æµÄøńµćŹż¼ĒĪŖN£¬±ß½ēÉĻµÄøńµćŹż¼ĒĪŖL£¬ĄżČē£¬Ķ¼ÖŠČż½ĒŠĪABCŹĒøńµćČż½ĒŠĪ£¬ĘäÖŠS=2£¬N=0£¬L=6£»Ķ¼ÖŠøńµć¶ą±ßŠĪDEFGHIĖł¶ŌÓ¦µÄS£¬N£¬L·Ö±šŹĒ £® ¾Ģ½¾æ·¢ĻÖ£¬ČĪŅāøńµć¶ą±ßŠĪµÄĆ껿SæɱķŹ¾ĪŖS=aN+bL+c£¬ĘäÖŠa£¬b£¬cĪŖ³£Źż£¬Ōņµ±N=5£¬L=14Ź±£¬S= £® £ØÓĆŹżÖµ×÷“š£©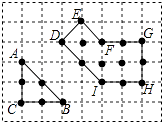
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDÖŠ£¬”ĻB£½90”ć£¬AB”ĪCD£¬MĪŖBC±ßÉĻµÄŅ»µć£¬ĒŅAMĘ½·Ö”ĻBAD£¬DMĘ½·Ö”ĻADC.

(1)ĒóÖ¤£ŗAM”ĶDM£»
(2)ČōBC£½8£¬ĒóµćMµ½ADµÄ¾ąĄė£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,½«±ß³¤ĪŖ2cmµÄÕż·½ŠĪABCDŃŲĘä¶Ō½ĒĻßAC¼ōæŖ,ŌŁ°Ń”÷ABCŃŲ×ÅAD·½ĻņĘ½ŅĘ,µĆµ½”÷A”ÆB”ÆC”Æ,ČōĖüŅĘ¶ÆµÄ¾ąĄėAA”ƵČÓŚ1cm,ŌņĮ½øöČż½ĒŠĪÖŲµž²æ·ÖµÄĆ껿ĪŖ____________cm2.
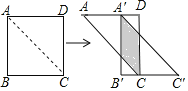
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ¹ŲÓŚx£¬yµÄ¶žŌŖŅ»“Ī·½³Ģ×é ![]() ÖŠ£®
ÖŠ£®
£Ø1£©Čōa=3£®Ēó·½³Ģ×éµÄ½ā£»
£Ø2£©ČōS=a£Ø3x+y£©£¬µ±aĪŖŗĪÖµŹ±£¬SÓŠ×īÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚŅ»øöĶ¼ŠĪ,ĶعżĮ½ÖÖ²»Ķ¬µÄ·½·Ø¼ĘĖćĖüµÄĆ껿,æÉŅŌµĆµ½Ņ»øöŹżŃ§µČŹ½,ĄżČēĶ¼1æÉŅŌµĆµ½(a+b)2=a2+2ab+b2,Ēė½ā“šĻĀĮŠĪŹĢā£ŗ

£Ø1£©Š“³öĶ¼2ÖŠĖł±ķŹ¾µÄŹżŃ§µČŹ½”” ”””£
£Ø2£©øł¾ŻÕūŹ½³Ė·ØµÄŌĖĖć·ØŌņ,Ķعż¼ĘĖćŃéÖ¤ÉĻŹöµČŹ½”£
£Ø3£©ĄūÓĆ£Ø1£©ÖŠµĆµ½µÄ½įĀŪ,½ā¾öĻĀĆęµÄĪŹĢā£ŗ
Čōa+b+c=10,ab+ac+bc=35,Ōņa2+b2+c2= .
£Ø4£©Š”Ć÷Ķ¬Ń§ÓĆĶ¼3ÖŠxÕű߳¤ĪŖaµÄÕż·½ŠĪ,yÕű߳¤ĪŖbµÄÕż·½ŠĪzÕű߳¤·Ö±šĪŖa”¢bµÄ³¤·½ŠĪÖ½Ę¬Ę“³öŅ»øöĆ껿ĪŖ(5a+7b)(9a+4b)³¤·½ŠĪ,Ōņx+y+z=”” ”””£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ÕżĮł±ßŠĪÓ²Ö½Ę¬ABCDEFŌŚ×ĄĆęÉĻÓÉĶ¼1µÄĘšŹ¼Ī»ÖĆŃŲÖ±Ļßl²»»¬ŠŠµŲ·¹öŅ»ÖÜŗóµ½Ķ¼2Ī»ÖĆ£®ČōÕżĮł±ßŠĪµÄ±ß³¤ĪŖ2cm£¬ŌņÕżĮł±ßŠĪµÄÖŠŠÄOŌĖ¶ÆµÄĀ·³ĢĪŖcm£® 
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com