下列三组正多边形的组合:①正八边形和正方形,②正五边形和正八边形,③正六边形和正方形.能够铺满地面的组合是① 题目和参考答案——青夏教育精英家教网—

9．下列三组正多边形的组合：①正八边形和正方形；②正五边形和正八边形；③正六边形和正方形，能够铺满地面的组合是①（填序号即可）

分析能够铺满地面的图形，即是能够凑成360°的图形组合．

解答解：①正方形的每个内角为90°，正八边形的每个内角为135°，两个正八边形和一个正方形刚好能铺满地面；
②正五边形每个内角是180°-360°÷5=108°，正八边形每个内角为135度，135m+108n=360°，显然n取任何正整数时，m不能得正整数，故不能铺满；
③正六边形的每个内角是120°，正方形的每个内角是90°，120m+90n=360°，显然n取任何正整数时，m不能得正整数，故不能铺满；
故答案为：①．

点评此题主要考查了平面镶嵌，解这类题，除了掌握多边形镶嵌成平面图形的条件，还可列二元方程看是否有正整数解来判断．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

19．已知正方形OABC的边OC、OA分别在x、y轴的正半轴上，点B坐标为（10，10），点P从O出发沿O→C→B运动，速度为1个单位每秒，连接AP．设运动时间为t．
（1）若抛物线y=-（x-h）²+k经过A、B两点，求抛物线函数关系式；
（2）当0≤t≤10时，如图1，过点O作OH⊥AP于点H，直线OH交边BC于点D，连接AD，PD，设△APD的面积为S，求S的最小值；
（3）在图2中以A为圆心，OA长为半径作⊙A，当0≤t≤20时，过点P作PQ⊥x轴（Q在P的上方），且线段PQ=t+12：
①当t在什么范围内，线段PQ与⊙A只有一个公共点？当t在什么范围内，线段PQ与⊙A有两个公共点？
②请将①中求得的t的范围作为条件，证明：当t取该范围内任何值时，线段PQ与⊙A总有两个公共点．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．在正方形ABCD中，AB=2，．
（1）如图1，点P是对角线AC上任一点，若M是AB中点，求PM+PB的最小值；
（2）如图2，点P是对角线AC上任一点，若M，N分别是边AB，BC上的点，且AM=$\frac{1}{2}$AB，CN=$\frac{1}{3}$BC，求PM+PN的最小值．
（3）如图3，若M₁，M₂是AB边三等分点，P₁，P₂是对角线AC上任意两点，求（P₁B+P₁M₁）²+（P₂M₁+P₂M₂）²的最小值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

17．计算
（1）解方程组$\left\{\begin{array}{l}{x-y=13}\\{x=6y-7}\end{array}\right.$
（2）解不等式组$\left\{\begin{array}{l}{5x-9＜3（x-1）}\\{1-\frac{3}{2}x≤\frac{1}{2}x-1}\end{array}\right.$．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

4．若关于x的不等式组$\left\{\begin{array}{l}{x-a＞0}\\{1-2x＞x-2}\end{array}\right.$的解集中只有4个整数解，则a取值范围是-4≤a＜-3．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

14．

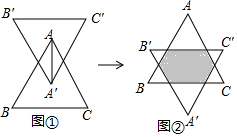如图①，等边三角形ABC和等边三角形A′B′C′的边长均为2，且BC∥B′C′，将等边三角形ABC沿A′A方向向上平移到图②的位置，则阴影部分的周长为4．