
【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.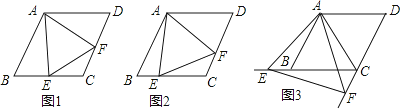
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
【答案】
(1)
解:结论AE=EF=AF.理由:如图1中 
,连接AC,
∵四边形ABCD是菱形,∠B=60°,
∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ADC是等边三角形,
∴∠BAC=∠DAC=60°
∵BE=EC,
∴∠BAE=∠CAE=30°,AE⊥BC,
∵∠EAF=60°,
∴∠CAF=∠DAF=30°,
∴AF⊥CD,
∴AE=AF(菱形的高相等),
∴△AEF是等边三角形,
∴AE=EF=AF.
(2)
解:证明:如图2中 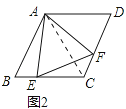
,∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAE,
在△BAE和△CAF中,
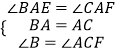 ,
,
∴△BAE≌△CAF,
∴BE=CF.
(3)
解: 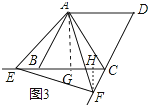
过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,
∵∠EAB=15°,∠ABC=60°,
∴∠AEB=45°,
在RT△AGB中,∵∠ABC=60°AB=4,
∴BG=2,AG=2 ![]() ,
,
在RT△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2 ![]() ,
,
∴EB=EG﹣BG=2 ![]() ﹣2,
﹣2,
∵△AEB≌△AFC,
∴AE=AF,EB=CF=2 ![]() ﹣2,∠AEB=∠AFC=45°,
﹣2,∠AEB=∠AFC=45°,
∵∠EAF=60°,AE=AF,
∴△AEF是等边三角形,
∴∠AEF=∠AFE=60°
∵∠AEB=45°,∠AEF=60°,
∴∠CEF=∠AEF﹣∠AEB=15°,
在RT△EFH中,∠CEF=15°,
∴∠EFH=75°,
∵∠AFE=60°,
∴∠AFH=∠EFH﹣∠AFE=15°,
∵∠AFC=45°,∠CFH=∠AFC﹣∠AFH=30°,
在RT△CHF中,∵∠CFH=30°,CF=2 ![]() ﹣2,
﹣2,
∴FH=CFcos30°=(2 ![]() ﹣2)
﹣2) ![]() =3﹣
=3﹣ ![]() .
.
∴点F到BC的距离为3﹣ ![]() .
.
【解析】(1)结论AE=EF=AF.只要证明AE=AF即可证明△AEF是等边三角形.
(2)欲证明BE=CF,只要证明△BAE≌△CAF即可.(3)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,根据FH=CFcos30°,因为CF=BE,只要求出BE即可解决问题. 本题考查四边形综合题、菱形的性质、等边三角形的判定、全等三角形的判定和性质等知识,解题的关键是灵活应用这些知识解决问题,学会添加常用辅助线,属于中考压轴题.
【考点精析】通过灵活运用菱形的性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.


科目:初中数学 来源: 题型:
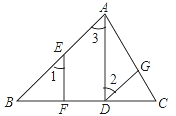
【题目】如图,已知△ABC中,AD⊥BC于点D,E为AB边上任意一点,EF⊥BC于点F,∠1=∠2.求证:DG∥AB.请把证明的过程填写完整.
证明:∵AD⊥BC,EF⊥BC( ),
∴∠EFB=∠ADB=90°(垂直的定义)
∴EF∥ ( )
∴∠1= ( )
又∵∠1=∠2(已知)
∴ ( )
∴DG∥AB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A( ![]() ,
, ![]() ),点D的坐标为(0,1)
),点D的坐标为(0,1) 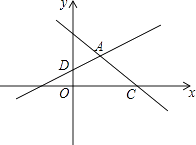
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
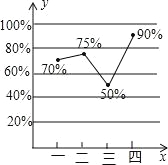
【题目】某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:
(1)若第一季度的汽车销售量为2100辆,求该季的汽车产量;
(2)圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
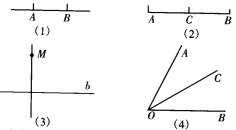
【题目】看图填空:
(1)过点________和点_______作直线;
(2)延长线段________到_________,且使________=_________.
(3)过点_________作直线_______的垂线;
(4)作射线_______,使_____平分∠________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.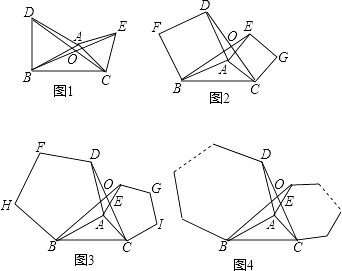
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC= ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC和△BDE都是等边三角形.则下列结论:①AE=CD;②BF=BG;③∠AHC=60°;④△BFG是等边三角形;⑤HB平分∠AHD.其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去新华书店,如图表示他离家的距离y(千米)与所用的时间s(小时)之间关系的函数图象 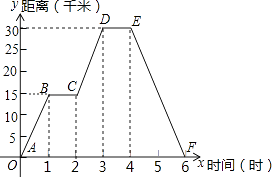
(1)根据图象回答:小明家离新华书店千米,小明用了小时到达新华书店;
(2)小明从家出发两个半小时走了千米;
(3)直线CD的函数解析式为;
(4)小明出发小时,离家12千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com