

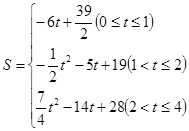
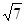 £©
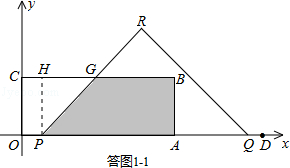
£©
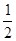 £Ø2t+2t+3£©”Į3
£Ø2t+2t+3£©”Į3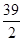 £»
£»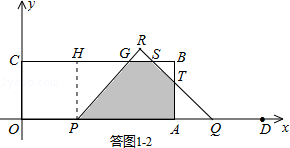
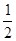 £Ø2t+2t+3£©”Į3©
£Ø2t+2t+3£©”Į3©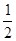 £Øt©1£©2
£Øt©1£©2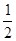 t2©5t+19£»
t2©5t+19£»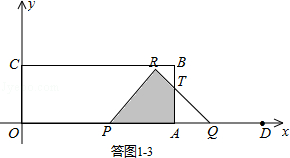
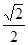 £Ø12©3t£©£®
£Ø12©3t£©£®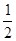 PR2©
PR2©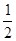 AQ2
AQ2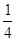 £Ø12©3t£©2©
£Ø12©3t£©2©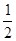 £Ø4©t£©2
£Ø4©t£©2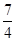 t2©14t+28£®
t2©14t+28£®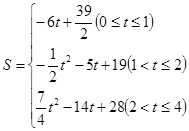 £®
£®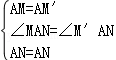
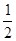 PQ=
PQ=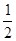 £Ø12©3t£©£¬
£Ø12©3t£©£¬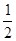 PQ=
PQ=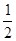 £Ø12©3t£©£¬AQ=4©t£¬
£Ø12©3t£©£¬AQ=4©t£¬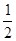 £Ø12©3t£©©£Ø4©t£©=©
£Ø12©3t£©©£Ø4©t£©=©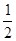 t+2£®
t+2£®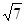 »ņn=©2©
»ņn=©2©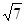 £ØÉįČ„£©
£ØÉįČ„£©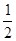 t=©2+
t=©2+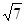
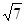 £®
£®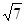 £©Ćė£®
£©Ćė£®

 Ó¦ÓĆĢā×÷Ņµ±¾ĻµĮŠ“š°ø
Ó¦ÓĆĢā×÷Ņµ±¾ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
 x2+bx+cµÄĶ¼Ļó½»xÖįÓŚA”¢DĮ½µć£¬²¢¾¹żBµć£¬ŅŃÖŖAµć×ų±źŹĒ£Ø2£¬0£©£¬BµćµÄ×ų±źŹĒ£Ø8£¬6£©£®
x2+bx+cµÄĶ¼Ļó½»xÖįÓŚA”¢DĮ½µć£¬²¢¾¹żBµć£¬ŅŃÖŖAµć×ų±źŹĒ£Ø2£¬0£©£¬BµćµÄ×ų±źŹĒ£Ø8£¬6£©£® S”÷BCD£æČō“ęŌŚ£¬ĒėĒó³öPµćµÄ×ų±ź£»Čō²»“ęŌŚ£®ĒėĖµĆ÷ĄķÓÉ£®
S”÷BCD£æČō“ęŌŚ£¬ĒėĒó³öPµćµÄ×ų±ź£»Čō²»“ęŌŚ£®ĒėĖµĆ÷ĄķÓÉ£®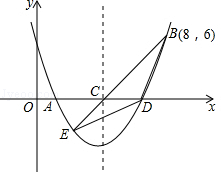
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
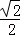 Ź±£¬ĒóµćEµÄ×ų±ź£»
Ź±£¬ĒóµćEµÄ×ų±ź£»
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
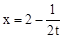 £¬¶„µćĖę×ÅtµÄŌö“óĻņÉĻŅĘ¶ÆŹ±£¬ĒótµÄȔֵ·¶Ī§£®
£¬¶„µćĖę×ÅtµÄŌö“óĻņÉĻŅĘ¶ÆŹ±£¬ĒótµÄȔֵ·¶Ī§£®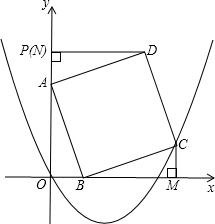
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
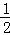 x2+mx+nÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻߵĶŌ³ĘÖį½»xÖįÓŚµćD£¬ŅŃÖŖA£Ø©1£¬0£©£¬C£Ø0£¬2£©£®
x2+mx+nÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻߵĶŌ³ĘÖį½»xÖįÓŚµćD£¬ŅŃÖŖA£Ø©1£¬0£©£¬C£Ø0£¬2£©£®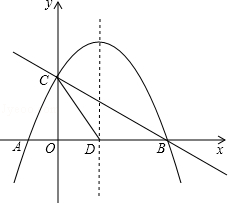
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
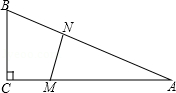
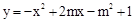 ÓėxÖį½»µćĪŖA”¢B£ØµćBŌŚµćAµÄÓŅ²ą£©£¬ÓėyÖį½»ÓŚµćC£®
ÓėxÖį½»µćĪŖA”¢B£ØµćBŌŚµćAµÄÓŅ²ą£©£¬ÓėyÖį½»ÓŚµćC£®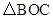 ŹĒµČŃüČż½ĒŠĪ£¬ĒóÅ×ĪļĻߵĽāĪöŹ½£»
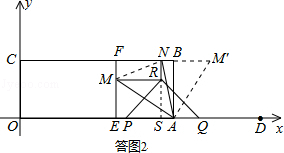
ŹĒµČŃüČż½ĒŠĪ£¬ĒóÅ×ĪļĻߵĽāĪöŹ½£»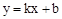 £¬µćP£Øn£¬0£©ŹĒxÖįÉĻŅ»øö¶Æµć£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬¹żµćP×÷“¹Ö±ÓŚxÖįµÄÖ±Ļß½»ÕāøöŅ»“ĪŗÆŹżµÄĶ¼ĻóÓŚµćM£¬½»Å×ĪļĻß
£¬µćP£Øn£¬0£©ŹĒxÖįÉĻŅ»øö¶Æµć£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬¹żµćP×÷“¹Ö±ÓŚxÖįµÄÖ±Ļß½»ÕāøöŅ»“ĪŗÆŹżµÄĶ¼ĻóÓŚµćM£¬½»Å×ĪļĻß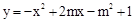 ÓŚµćN£¬ČōÖ»ÓŠµ±
ÓŚµćN£¬ČōÖ»ÓŠµ±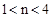 Ź±£¬µćMĪ»ÓŚµćNµÄĻĀ·½£¬ĒóÕāøöŅ»“ĪŗÆŹżµÄ½āĪöŹ½£®
Ź±£¬µćMĪ»ÓŚµćNµÄĻĀ·½£¬ĒóÕāøöŅ»“ĪŗÆŹżµÄ½āĪöŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com