
 如图,在矩形ABCD中,M,N分别是AD,BC的中点,P,Q分别是BM,DN的中点
如图,在矩形ABCD中,M,N分别是AD,BC的中点,P,Q分别是BM,DN的中点分析 (1)因为M,N分别是AD,BC的中点,由矩形的性质可得DM=BN,DM∥BN,利用平行四边形的判定定理可得结论;
(2)由四边形DMBN是平行四边形,求出BM=DN,BM∥DN,求出三角形MPNQ是平行四边形,根据直角三角形斜边上中线性质求出MQ=NQ,根据菱形判定推出即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵M、N分别AD、BC的中点,
∴DM=BN,
∴四边形DMBN是平行四边形;
(2)解:四边形MPNQ是菱形.
∵四边形DMBN是平行四边形,
∴BM=DN,BM∥DN,
∵P、Q分别BM、DN的中点,
∴MP=NQ,MP∥NQ,
∴四边形MPNC是平行四边形,
连接MN,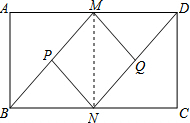
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵M、N分别AD、BC的中点,
∴DM=CN,
∴四边形DMNC是矩形,
∴∠DMN=∠C=90°,
∵Q是DN中点,
∴MQ=NQ,
∴四边形MPNQ是菱形.
点评 本题考查了平行四边形的性质和判定,菱形的判定,矩形的性质,综合运用各性质定理是解答此题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知由几个大小相同的小立方块搭成的几何体,从上面观察,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请分别画出从正面、左面看到的这个几何体的形状图.(几何体中每个小立方块的棱长都是1cm)
已知由几个大小相同的小立方块搭成的几何体,从上面观察,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请分别画出从正面、左面看到的这个几何体的形状图.(几何体中每个小立方块的棱长都是1cm)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,有两棵树,一棵高AD=6米,另一棵高BC=2米,两树相距DC=8米,一只小鸟从一棵树的树梢B飞到另一棵树的树梢A,至少飞了4$\sqrt{5}$米.
如图所示,有两棵树,一棵高AD=6米,另一棵高BC=2米,两树相距DC=8米,一只小鸟从一棵树的树梢B飞到另一棵树的树梢A,至少飞了4$\sqrt{5}$米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com