
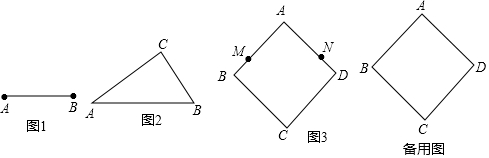
���� ��1��ȡAB���е�O����OΪԲ�ģ���ABΪ�뾶��Բ����Բ������ȡһ��C����E��F���⣩������������ABC���ɵ÷��������������Σ�
��2��������BD���ֱ���BD��ACΪ2���ɵý��ۣ�
��3����Ϊ��M��AB��ʱ����AMN�ǵ���ֱ�������Σ��������ǡ���г�����Ρ���
���Է���������������ۣ�
�����ױ�MN������AE=MNʱ����ͼ3������AE=MN����ʽ��s��ֵ��
������AM����������NG��ȣ���AM=GN=ANʱ������tan��HMN=$\frac{HN}{MH}$=$\frac{\sqrt{15}}{3}$��tan��AME=$\frac{AE}{ME}$=$\frac{s}{2-s}$����ʽ�ɵ�s��ֵ��
���  �⣺��1����ͼ1��
�⣺��1����ͼ1��
�����߶�AB���е�O��
���Ե�OΪԲ�ģ�AB��Ϊ�뾶��Բ��
����ԲO��ȡһ��C����E��F���⣩������AC��BC��
���ABC����������������
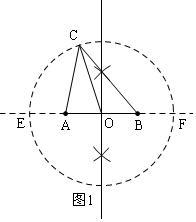
��2����ͼ2����C=90�㣬AB=$\sqrt{7}$��BC=$\sqrt{3}$��
��AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{��\sqrt{7}��^{2}-��\sqrt{3}��^{2}}$=2��
ȡAC���е�D������BD��
��CD=1��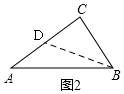
��Rt��BCD��
�ɹ��ɶ����ã�BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=2��
������BD=��AC��
���ABC�ǡ���г�����Ρ���
��3����֪����M��AB��ʱ����AMN�ǵ���ֱ�������Σ��������ǡ���г�����Ρ���
��M��BC��ʱ������AC��MN�ڵ�E��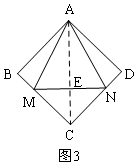
�����ױ�MN������AE=MNʱ����ͼ3��
������ã�AC=$\sqrt{2}$��MC=2-S��
�߶���M��N�ӵ�Aͬʱ����������ͬ�ٶ��˶���
��AB+BM=DN+AD��
��MC=CN��
���MCN�ǵ���ֱ�������Σ�
��MN=$\sqrt{2}$MC=$\sqrt{2}$��2-s����CE=$\frac{1}{2}$MN=$\frac{\sqrt{2}}{2}$��2-S����
��AE=MN��
��$\sqrt{2}-\frac{\sqrt{2}}{2}��2-s��=\sqrt{2}��2-s��$��S=$\frac{4}{3}$��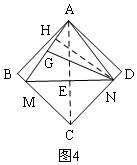
������AM����������NG��ȣ���AM=GN=ANʱ��
��NH��AM��H����ͼ4��
��NG=NA��NH��AM��
��GH=AH=$\frac{1}{2}$AG=$\frac{1}{4}$AM��
��Rt��NHA��
NH=$\sqrt{A{N}^{2}-��\frac{1}{4}AM��^{2}}$=$\sqrt{A{M}^{2}-��\frac{1}{4}AM��^{2}}$=$\frac{\sqrt{15}}{4}AM$��
��Rt��NHM��tan��HMN=$\frac{HN}{MH}$=$\frac{\frac{\sqrt{15}}{4}AM}{\frac{3}{4}AM}$=$\frac{\sqrt{15}}{3}$��
��Rt��AME��tan��AME=$\frac{AE}{ME}$=$\frac{\sqrt{2}-\frac{\sqrt{2}}{2}��2-s��}{\frac{\sqrt{2}}{2}��2-s��}$=$\frac{s}{2-s}$��
�� $\frac{s}{2-s}=\frac{\sqrt{15}}{3}$��
s=5-$\sqrt{15}$��
���ϣ�S=$\frac{4}{3}$��5-$\sqrt{15}$ʱ��
���� ���⿼���ı����ۺ��⡢�����ε����ߵĶ��塢�����ε����ʡ�����ֱ�������ε��ж������ʡ�������Ǻ��������ɶ�����֪ʶ������Ĺؼ����������⣬ѧ���÷��̵�˼��˼�����⣬�����п�������Ŀ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
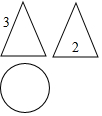 ��ͼ��һ�������������ͼ��ͼ�гߴ絥λ��cm��������ͼ����ʾ���ݼ������������IJ����Ϊ��������cm2��
��ͼ��һ�������������ͼ��ͼ�гߴ絥λ��cm��������ͼ����ʾ���ݼ������������IJ����Ϊ��������cm2��| A�� | 3�� | B�� | 6�� | C�� | 9�� | D�� | 12�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 900�� | B�� | 360�� | C�� | 540�� | D�� | 720�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��Ʒ�� | A | B | C |
| ÿ���������������֣� | 2.2 | 2.1 | 2 |
| ÿ���ۻ�������Ԫ�� | 6 | 8 | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
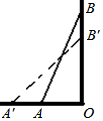 ��ͼ������AB����ǽ�ϣ����ӵ�A��ǽ��O�ľ���Ϊ2m�����ӵĶ���B������ľ���Ϊ7m���ֽ����ӵĵ�A�����ƶ���A�䣬ʹ���ӵĵ�A�䵽ǽ��O�ľ������3m��ͬʱ���ӵĶ���B�½���B�䣬��ôBB�䣨������
��ͼ������AB����ǽ�ϣ����ӵ�A��ǽ��O�ľ���Ϊ2m�����ӵĶ���B������ľ���Ϊ7m���ֽ����ӵĵ�A�����ƶ���A�䣬ʹ���ӵĵ�A�䵽ǽ��O�ľ������3m��ͬʱ���ӵĶ���B�½���B�䣬��ôBB�䣨������| A�� | С��1 m | B�� | ����1 m | C�� | ����1 m | D�� | С�ڻ����1 m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3.14 | B�� | $\sqrt{16}$ | C�� | $\frac{2}{3}$ | D�� | $\sqrt{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
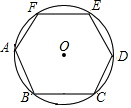 ��������ABCDEF�ڽ��ڡ�O���������ε��ܳ���12�����O�İ뾶�ǣ�������
��������ABCDEF�ڽ��ڡ�O���������ε��ܳ���12�����O�İ뾶�ǣ�������| A�� | $\sqrt{3}$ | B�� | 2 | C�� | 2$\sqrt{2}$ | D�� | 2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com