
【题目】如图,抛物线y=ax2+bx+c经过A(﹣4,0)、B(1,0)、C(0,3)三点,直线y=mx+n经过A(﹣4,0)、C(0,3)两点. 
(1)写出方程ax2+bx+c=0的解;
(2)若ax2+bx+c>mx+n,写出x的取值范围.
【答案】
(1)解:∵抛物线y=ax2+bx+c经过A(﹣4,0)、B(1,0),
∴方程ax2+bx+c=0的解为x1=﹣4,x2=1
(2)解:由图可知,ax2+bx+c>mx+n时,﹣4<x<0
【解析】(1)根据一元二次方程的解就是抛物线与x轴的交点的横坐标解答即可;(2)确定出抛物线在直线上方部分的x的取值即可.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】正方形OABC的边长为1,把它放在如图所示的直角坐标系中,点M(t,0)是x轴上一个动点(t≥1),连接BM,在BM的右侧作正方形BMNP;直线DE的解析式为y=2x+b,与x轴交于点D,与y轴交于点E,当△PDE为等腰直角三角形时,点P的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC四个顶点的坐标分别为O(0,0),A(﹣3,0),B(﹣4,2),C(﹣1,2).将四边形OABC绕点O顺时针旋转90°后,点A,B,C分别落在点A′,B′,C′处. 
(1)请你在所给的直角坐标系中画出旋转后的四边形OA′B′C′;
(2)点C旋转到点C′所经过的弧的半径是 , 点C经过的路线长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年我县某校有若干名学生参加了七年级数学期末测试,学校随机抽取了考生总数的10%的学生数学成绩,现将他们的成绩分成:A(96分~120分)、B(84分~95分)、C(72分~83分)、D(72分以下)四个等级进行分析,并根据成绩得到如下两个统计图:


(1)在所抽取的考生中,若D级只有3人:
①请估算该校所有考生中,约有多少人数学成绩是D级?
②考生数学成绩的中位数落在__________等级中;
(2)有一位同学在计算所抽取的考生数学成绩的平均数时,其方法是:![]() =
=![]() =76.25,
=76.25,
问这位同学的计算正确吗?若不正确,请你帮他计算正确的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在同心圆中,大圆的弦AB交小圆于C,D两点. 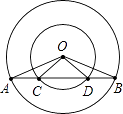
(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段AB绕点A逆时针旋转60°得AC,连接BC,作△ABC的外接圆⊙O,点P为劣弧 ![]() 上的一个动点,弦AB,CP相交于点D.
上的一个动点,弦AB,CP相交于点D. 
(1)求∠APB的大小;
(2)当点P运动到何处时,PD⊥AB?并求此时CD:CP的值;
(3)在点P运动过程中,比较PC与AP+PB的大小关系,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(﹣1,0),点B(0,﹣2),AD与y轴交于点E,且E为AD的中点,双曲线y=![]() 经过C,D两点且D(a,4)、C(2,b).
经过C,D两点且D(a,4)、C(2,b).
(1)求a、b、k的值;
(2)如图2,线段CD能通过旋转一定角度后点C、D的对应点C′、D′还能落在y=![]() 的图象上吗?如果能,写出你是如何旋转的,如果不能,请说明理由;
的图象上吗?如果能,写出你是如何旋转的,如果不能,请说明理由;
(3)如图3,点P在双曲线y=![]() 上,点Q在y轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试求满足要求的所有点P、Q的坐标.
上,点Q在y轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试求满足要求的所有点P、Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,![]() 的平行线
的平行线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)请指出图中平行四边形的个数,并说明理由;
(2)![]() 与
与![]() 相等吗?为什么?
相等吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E. 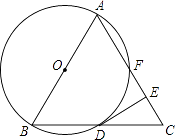
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com