【题目】用方程解答下列问题
（1）一件工作，甲单独做20小时完成，乙单独做12小时完成，现在先由甲单独做4小时，余下的由甲乙一起完成余下的部分需要几小时完成？
（2）王强参加了一场3000米的赛跑，他以6米/秒的速度跑了一段路程，又以4米/秒的速度跑完了其余的路程，一共花了10分钟，王强以6米秒的速度跑了多少米？
【答案】（1）余下的部分需要6小时完成；（2）王强以6米/秒的速度跑了1800米．
【解析】
（1）先假设该项工作为整体1，那么甲1小时做工作的
，乙1小时做工作的
．再设余下部分共用x小时．则根据题意列式即可；
（2）设王强以6米/秒的速度跑了x米，依据题意建立方程关系即可得到结论．
（1）设余下的部分需要x小时完成，×4+（
）x＝1，
解得x＝6．
答：余下的部分需要6小时完成；
（2）设王强以6米/秒速度跑了x秒，则王强以4米/秒速度跑了（3000﹣x）秒．
根据题意列方程
即2x+3（3000-x）=10×60×12，
则2x+9000-3x=7200，
即x=1800．
答：王强以6米/秒的速度跑了1800米．
科目：初中数学 来源： 题型：
【题目】粮库6天内发生粮食进、出库的吨数如下（“
”表示进库，“
”表示出库）：
，
，
，
，
，
．
（1）经过这6天，库里的粮食是增多还是减少了?增加（减少）了多少?
（2）经过这6天，管理员结算时发现库里还存480吨粮，那么6天前库里存粮多少吨?
（3）如果进出的装卸费都是每吨5元，那么这6天要付多少装卸费?
查看答案和解析>>
科目：初中数学 来源： 题型：
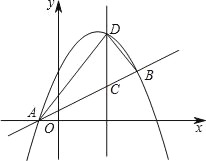
【题目】如图，抛物线y=ax2+bx+
与直线AB交于点A（﹣1，0），B（4，），点D是抛物线A、B两点间部分上的一个动点（不与点A、B重合），直线CD与y轴平行，交直线AB于点C，连接AD，BD．
（1）求抛物线的表达式；
（2）设点D的横坐标为m，△ADB的面积为S，求S关于m的函数关系式，并求出当S取最大值时的点C的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一个长方形运动场被分隔成
、
、
、
、
共
个区， 
区是边长为
的正方形， 
区是边长为
的正方形．
（1）列式表示每个
区长方形场地的周长，并将式子化简；
（2）列式表示整个长方形运动场的周长，并将式子化简；
（3）如果
， 
，求整个长方形运动场的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，BA=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．
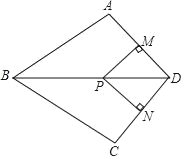
（1)求证：点A与C关于直线BD对称.
(2)若∠ADC=90°，求证四边形MPND为正方形.
查看答案和解析>>
科目：初中数学 来源： 题型：
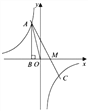
【题目】如图，已知反比例函数
的图象经过第二象限内的点A（
，4），AB⊥x轴于点B，△AOB的面积为2,若直线
经过点A，并且经过反比例函数的图象上另一点C（2，
）．
（1）求反比例函数和直线的解析式；
（2）设直线与
轴交于点M，求AM的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，CE∥BF，CE=BF．则添加下列条件还不能使△EAC≌△FDB．（ ）
A. AB=CDB. AE∥DFC. ∠E=∠FD. AE=DF
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图：O是直线AB上一点，∠AOC＝50°,OD是∠BOC的角平分线，OE⊥OC于点O.求∠DOE的度数.（请补全下面的解题过程）
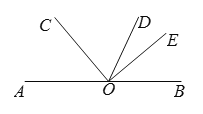
解：∵O是直线AB上一点，∠AOC＝50°，
∴∠BOC＝180°－∠AOC＝ °.
∵ OD是∠BOC的角平分线，
∴∠COD＝ ∠BOC .( )
∴∠COD＝65°.
∵OE⊥OC于点O，（已知）.
∴∠COE＝ °.( )
∴∠DOE＝∠COE－∠COD＝ ° .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在四边形ABCD中，AD∥BC，∠A=∠C，点P在边AB上．
（1）求证：四边形ABCD是平行四边形；
（2）若AB=AD，以过点P的直线为轴，将四边形ABCD折叠，使点B、C分别落在点B′、C′上，且B′C′经过点D，折痕与四边形的另一交点为Q．在图2中作出四边形PB′C′Q（保留作图痕迹，不必说明作法和理由）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com