练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．计算：
    （1）${（\sqrt{3}-5）^2}$
    （2）$\sqrt{54}a+\sqrt{5}b-\sqrt{20}b-3\sqrt{6}b$．

    分析 （1）利用完全平方公式计算；
    （2）先把各二次根式化简为最简二次根式，然后合并即可．

    解答 解：（1）原式=3-10$\sqrt{3}$+25=28-10$\sqrt{3}$；
    （2）原式=3$\sqrt{6}$a+$\sqrt{5}$b-2$\sqrt{5}$b-3$\sqrt{6}$b
    =3$\sqrt{6}$a-（$\sqrt{5}$+3$\sqrt{6}$）b．

    点评 本题考查了二次根式的混合运算：先把各二次根式化简为最简二次根式，然后进行二次根式的乘除运算，再合并即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

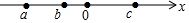    18．实数a，b，c在数轴上对应的点如图，则下列式子中正确的是（　　）
    A．a-c＞b-cB．ac＞bcC．a+c＜b+cD．$\frac{a}{b}$＜$\frac{c}{b}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．在平面直角坐标系中，抛物线y=-（x-1）2+2的顶点坐标是（　　）
    A．（-1，2）B．（1，2）C．（2，-1）D．（2，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，锐角△ABC是⊙O内接三角形，弦AE⊥BC，垂足为D．在AD上取点F，使FD=DE，连接CF，并延长交AB于点G．求证：CG⊥AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，大正方形的边长为a，小正方形的边长为b．
    （1）求阴影部分的面积S．
    （2）如果a+b=4，ab=2，求S的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．写出5个数（不允许重复），同时满足下列4个条件：
    ①有1个数既不是正数，也不是负数；
    ②其中3个不是负数；
    ③其中至少有1个是正分数；
    ④其中只有1个是负整数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费，如表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息：（水价计费=自来水销售费用+污水处理费用）
      自来水销售价格污水处理价格 
     每户每月用水量 单价：元/吨 单价：元/吨
     17吨及以下 a 0.80
     超过17吨不超过30吨的部分 b 0.80
     超过30吨的部分6.00 0.80
    已知小王家2014年2月份用水20吨，交水费66元；3月份用水25吨，交水费91元．
    （1）求a、b的值；
    （2）随着夏天的到来用水量将增加，为了节约开支，小王计划把6月份水费控制在家庭月收入的2%，若小王家月收入为9200元，则小王家6月份最多能用水多少吨？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．先阅读下列一段文字，然后解答问题：
    某食品研究部门欲将甲、乙、丙三种食物混合研制成100千克食物，并规定：研制成的混合食品中至少需含44000单位的维生素A和48000单位的维生素B，三种食物的维生素A、B的含量如表1所示：
    甲种
    食物    		乙种
    食物    		丙种
    食物    		每千克生产成本（元）
    甲种食物9
    维生素A（单位/千克）400600400乙种食物12
    维生素B（单位/千克）800200400丙种食物8
    （表1）（表2）
    设所取甲、乙、丙三种食物的质量分别为x千克、y千克、z千克，
    （1）试根据题意列出等式和不等式，并说明：①y≥20；②2x-y≥40；
    （2）设甲、乙、丙三种食物的生产成本如表2所示：①试用含x、y的代数式表示研制的混合食品的总成本P（元）；②如果限定混合食品中甲种食物的质量为40千克，试求此时总成本P的取值范围，并确定当P取最小值时，所取乙、丙两种食物的质量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．分解因式：x2+12x-189，分析：由于常数项数值较大，则将x2+12x-1变为完全平方公式，再运用平方差公式进行分解，这样简单易行．
    x2+12x-189=x2+2*6x+62-36-189
    =（x+6）2-225
    =（x+6）2-152
    =（x+6+15）（x+6-15）
    =（x+21）（x-9）
    请按照上面的方法分解因式：x2-60x+884．

    查看答案和解析>>

    同步练习册答案