
【题目】在![]() 中,
中,![]() ,
,![]() 为直线
为直线![]() 上一点,
上一点,![]() 为直线
为直线![]() 上一点,
上一点,![]() ,设
,设![]() ,
,![]() .
.
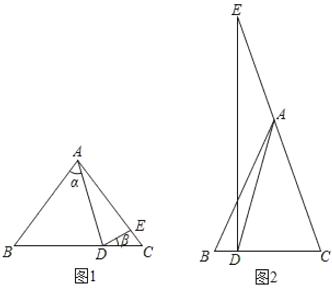
(1)如图1,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,则
上,则![]() ,
,![]() 之间关系式为__________.
之间关系式为__________.
(2)如图2,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在
在![]() 延长线上,则
延长线上,则![]() ,
,![]() 之间关系式为__________.
之间关系式为__________.
【答案】![]()
![]()
【解析】
(1)利用等腰三角形的性质和三角形的内角和即可得出结论;
(2)当点E在CA的延长线上,点D在线段BC上,同(1)的方法即可得出结论.
(1)设∠ABC=x,∠AED=y,
∵![]() ,
,![]() ,
,
∴∠ACB=∠ABC, ∠AED=∠ADE
∴∠ACB=x,∠ADE=y,
在△DEC中,∵∠ AED=∠ACB+∠EDC,
∴y=β+x,
在△ABD中,∵∠ADC=∠BAD+∠ABC, ∠ADC=∠ADE+∠EDC=∠AED+∠EDC,
∴α+x=y+β=β+x+β,
∴α=2β;
故答案为:α=2β;
(2)当点E在CA的延长线上,点D在线段BC上,
设∠ABC=x,∠ADE=y,
∵![]() ,
,![]() ,
,
∴∠ACB=∠ABC, ∠AED=∠ADE,
∴∠ACB=x,∠AED=y,
在△ABD中,∵∠ADC=∠BAD+∠ABC, ∠ADC=∠EDC-∠ADE,
∴x+α=β-y,
在△DEC中,∵∠ECD+∠CED+∠EDC=180°,
∴x+y+β=180°,
∴α=2β-180°;
故答案为α=2β-180°.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连结BF,交AC于点M,连结DE,BO.若∠BOC=60°,FO=FC,则下列结论:①AE=CF;②BF垂直平分线段OC;③△EOB≌△CMB;④四边形是BFDE菱形.其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,则△ABC的面积是
A.126 cm2 或66 cm2B.66 cm2C.120 cm2D.126cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个球,其中2个红球,2个白球,它们除颜色外其余都相同.
(1)摸出1个球是白球的概率是 ;
(2)同时摸两个球恰好是两个红球的概率(要求画树状图或列表).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
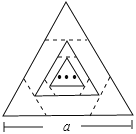
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
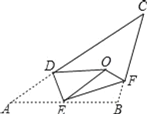
A. 40°B. 41°C. 42°D. 43°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+![]() …按此规律继续旋转,直至得到点P2018为止,则AP2018为( )
…按此规律继续旋转,直至得到点P2018为止,则AP2018为( )
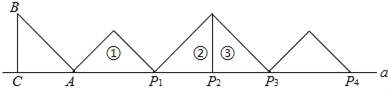
A. 1345+376![]() B. 2017+
B. 2017+![]() C. 2018+
C. 2018+![]() D. 1345+673
D. 1345+673![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小洋同学在笔记本上完成课堂练习的解题过程:
老师让同桌互相核对,同桌小宁和小洋的答案不一样,在仔细对比了自己和小洋书写的过程后,小宁说:“你在第一步出现了两个错误,导致最后错了.”小洋自己检查后发现,小宁说的是正确的.
解答下列问题:
(1)请你用标记符号“○”在以上小洋解答过程的第一步中错误之处;
(2)请重新写出完成此题的解答过程.
(2x+1)(2x﹣1)﹣(x﹣3)2
小洋的解答:
(2x+1)(2x﹣1)﹣(x﹣3)2
=(2x)2﹣1﹣(x2﹣3x+9) 第一步
=2x2﹣1﹣x2+3x﹣9 第二步
=x2+3x﹣10. 第三步
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的边OA,OC在坐标轴上,A(0,2),C(4,0).点P从点A出发,以每秒1个单位长度的速度沿射线AO方向运动,同时点Q从点C出发,以每秒2个单位的速度沿射线CO方向运动.设点P运动时间为t秒,(t>0)


(1)当t=1时,求△BPQ的周长;
(2)当t为何值时,△BPQ是等腰三角形;
(3)点C关于BQ的对称点为C’,当C’恰好落在直线AQ上时,△BPQ的面积为__________.(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com