
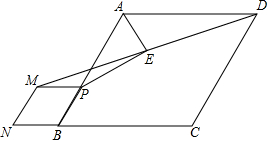
 如图,在菱形ABCD中,tan∠ABC=$\frac{4}{3}$,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则$\frac{AE}{PE}$的值为( )
如图,在菱形ABCD中,tan∠ABC=$\frac{4}{3}$,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则$\frac{AE}{PE}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
分析 如图,延长AE交MP的延长线于F,作AH⊥PF于H.证明△AED≌△FEM,可得AE=EF.AD=MF=AB,由PM=PB,推出PA=PF,推出PE⊥AF,∠APE=∠FPE,由∠APF=∠ABC,可得tan∠APE=tan∠ABC=$\frac{4}{3}$=$\frac{AH}{PH}$,设AH=4k,PH=3k,解直角三角形求出AE、PE即可解决问题.
解答 解:如图,延长AE交MP的延长线于F,作AH⊥PF于H.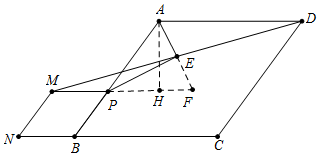
∵AD∥CN∥PM,
∴∠ADE=∠EMF,
∵ED=EM,∠AED=∠MEF,
∴△AED≌△FEM,
∴AE=EF.AD=MF=AB,
∵PM=PB,
∴PA=PF,
∴PE⊥AF,∠APE=∠FPE,
∵∠APF=∠ABC,
∴tan∠APE=tan∠ABC=$\frac{4}{3}$=$\frac{AH}{PH}$,设AH=4k,PH=3k,则PA=PF=5k,FH=2k,AF=$\sqrt{A{H}^{2}+H{F}^{2}}$=2$\sqrt{5}$k,
∵$\frac{1}{2}$•PF•AH=$\frac{1}{2}$•AF•PE,
∴PE=2$\sqrt{5}$k,AE=$\sqrt{5}$k
∴AE:PE=$\sqrt{5}$k:2$\sqrt{5}$=1:2,
故选C.
点评 本题考查全等三角形的判定和性质、菱形的性质、勾股定理、等腰三角形的判定和性质、平行线的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 “奔跑吧,兄弟!”节目组预设计一个新游戏:“奔跑”路线A、B、C、D四地,如图A、B、C三地在同一直线上,D在A北偏东30°方向,在C北偏西45°方向,C在A北偏东75°方向,且BD=BC=40m,从A地到D地的距离是20$\sqrt{6}$m.
“奔跑吧,兄弟!”节目组预设计一个新游戏:“奔跑”路线A、B、C、D四地,如图A、B、C三地在同一直线上,D在A北偏东30°方向,在C北偏西45°方向,C在A北偏东75°方向,且BD=BC=40m,从A地到D地的距离是20$\sqrt{6}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
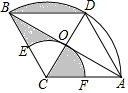 如图,菱形ACBD中,AB与CD交于点O,∠ACB=120°,以C为圆心、AC为半径作弧AB,再以C为圆心,CO为半径作弧EF分别交AC于点F、BC于点E,若CB=2,则图中阴影部分的面积为( )
如图,菱形ACBD中,AB与CD交于点O,∠ACB=120°,以C为圆心、AC为半径作弧AB,再以C为圆心,CO为半径作弧EF分别交AC于点F、BC于点E,若CB=2,则图中阴影部分的面积为( )| A. | $\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$ | B. | $\frac{π}{3}$-$\frac{1}{2}$ | C. | $\frac{2π}{3}$-$\frac{1}{2}$ | D. | π-$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
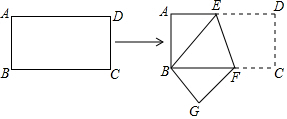 如图所示,长方形纸片ABCD的长AD=8cm,宽AB=4cm,将其折叠,使点D与点B重合.
如图所示,长方形纸片ABCD的长AD=8cm,宽AB=4cm,将其折叠,使点D与点B重合.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com