
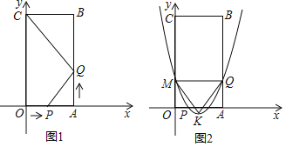
【题目】如图1,四边形OABC是矩形,点A的坐标为(3,0),点C的坐标为(0,6),点P从点O出发,沿OA以每秒1个单位长度的速度向点A出发,同时点Q从点A出发,沿AB以每秒2个单位长度的速度向点B运动,当点P与点A重合时运动停止.设运动时间为t秒.
(1)当t=2时,线段PQ的中点坐标为_____;
(2)当△CBQ与△PAQ相似时,求t的值;
(3)当t=1时,抛物线y=x2+bx+c经过P,Q两点,与y轴交于点M,抛物线的顶点为K,如图2所示,问该抛物线上是否存在点D,使∠MQD=![]() ∠MKQ?若存在,求出所有满足条件的D的坐标;若不存在,说明理由.
∠MKQ?若存在,求出所有满足条件的D的坐标;若不存在,说明理由.
【答案】(1)(![]() ,2);(2)
,2);(2)![]() 或
或![]() ;(3)存在;D(﹣
;(3)存在;D(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)根据点P,Q的运动速度找出当t=2时,点P,Q的坐标,再利用中点坐标公式即可求出此时线段PQ的中点坐标;
(2)根据点P,Q的运动速度找出运动时间为t秒时,PA,QA,QB,CB的值,由∠B=∠A=90°,可得出当![]() 或
或![]() 时,△CBQ与△PAQ相似,代入各线段的值即可求出t值;
时,△CBQ与△PAQ相似,代入各线段的值即可求出t值;
(3)当t=1时,先求出P,Q的坐标,然后求出抛物线的解析式,配方求出顶点K的坐标.分两种情况讨论,利用相似三角形的判定与性质求出HQ、OQ的解析式,再和抛物线解析式联立解方程组即可得出结论.
(1)当t=2时,点P的坐标为(2,0),点Q的坐标为(3,4),∴线段PQ的中点坐标为(![]() ),即(
),即(![]() ,2).
,2).
故答案为:(![]() ,2).
,2).
(2)当运动时间为t(0≤t≤3)秒时,点P的坐标为(t,0),点Q的坐标为(3,2t),∴PA=3﹣t,QA=2t,QB=6﹣2t,CB=3.
∵∠B=∠A=90°,∴当![]() 或
或![]() 时,△CBQ与△PAQ相似.
时,△CBQ与△PAQ相似.
①当![]() 时,
时,![]() ,解得:t1
,解得:t1![]() ,t2
,t2![]() (不合题意,舍去);
(不合题意,舍去);
②当![]() 时,
时,![]() ,解得:t
,解得:t![]() 或t=3(舍去).
或t=3(舍去).
综上所述:t的值为![]() 或
或![]() .
.
(3)当t=1时,P(1,0),Q(3,2),把P(1,0),Q(3,2)代入抛物线y=x2+bx+c中得:![]() ,解得:
,解得:![]() ,∴抛物线:y=x2﹣3x+2=
,∴抛物线:y=x2﹣3x+2=![]() ,∴顶点K(
,∴顶点K(![]() ,
,![]() ).
).
∵Q(3,2),M(0,2),∴MQ∥x轴.
作抛物线对称轴,交MQ于E,∴KM=KQ,KE⊥MQ,∴∠MKE=∠QKE=![]() ∠MKQ.
∠MKQ.
如图2,∠MQD=![]() ∠MKQ=∠QKE,设DQ交y轴于H.
∠MKQ=∠QKE,设DQ交y轴于H.
∵∠HMQ=∠QEK=90°,∴△KEQ∽△QMH,∴![]() ,∴
,∴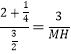 ,∴MH=2,∴H(0,4),易得HQ的解析式为:
,∴MH=2,∴H(0,4),易得HQ的解析式为:![]() ,则
,则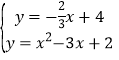 ,x2﹣3x+2=
,x2﹣3x+2=![]() ,解得:x1=3(舍),x2=
,解得:x1=3(舍),x2=![]() ,∴D(
,∴D(![]() ,
,![]() );
);
同理,在M的下方,y轴上存在点H,如图3,使∠HQM=![]() ∠MKQ=∠QKE.
∠MKQ=∠QKE.
由对称性得:H(0,0),易得OQ的解析式:![]() ,则
,则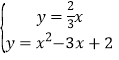 ,x2﹣3x+2=
,x2﹣3x+2=![]() ,解得:x1=3(舍),x2=
,解得:x1=3(舍),x2=![]() ,∴D(
,∴D(![]() ,
,![]() ).
).
综上所述:点D的坐标为:D(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】某农户承包荒山种了44棵苹果树.现在进入第三年收获期.收获时,先随意摘了5棵树上的苹果,称得每棵树摘得的苹果重量如下(单位:千克)35 35 34 39 37
(1)在这个问题中,总体指的是?个体指的是?样本是?样本容量是?
(2)试根据样本平均数去估计总体情况,你认为该农户可收获苹果大约多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由两个可以自由转动的转盘、每个转盘被分成如图所示的几个扇形、游戏者同时转动两个转盘,如果一个转盘转出了红色,另一转盘转出了蓝色,游戏者就配成了紫色下列说法正确的是( )

A. 两个转盘转出蓝色的概率一样大
B. 如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了
C. 先转动A 转盘再转动B 转盘和同时转动两个转盘,游戏者配成紫色的概率不同
D. 游戏者配成紫色的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
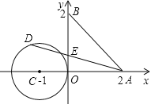
【题目】如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(﹣1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是( )
A. 2 B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
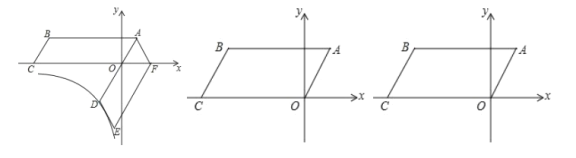
【题目】如图,在平面直角坐标系中,四边形![]() 为平行四边形,
为平行四边形,![]() 为坐标原点,
为坐标原点,![]() ,将平行四边形
,将平行四边形![]() 绕点
绕点![]() 逆时针旋转得到平行四边形
逆时针旋转得到平行四边形![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 落在
落在![]() 轴正半轴上.
轴正半轴上.
(1)证明:![]() 是等边三角形:
是等边三角形:
(2)平行四边形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 度
度![]() .
.![]() 的对应线段为
的对应线段为![]() ,点
,点![]() 的对应点为
的对应点为![]()
①直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标:
的坐标:
②对角线![]() 在旋转过程中设点
在旋转过程中设点![]() 坐标为
坐标为![]() ,当点
,当点![]() 到
到![]() 轴的距离大于或等于
轴的距离大于或等于![]() 时,求
时,求![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票。王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为 偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动。你认为这个方法公平吗?请画树状图或列表,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程![]() ,下列说法:①若a+c=0,方程
,下列说法:①若a+c=0,方程![]() 有两个不等的实数根;②若方程
有两个不等的实数根;②若方程![]() 有两个不等的实数根,则方程
有两个不等的实数根,则方程![]() 也一定有两个不等的实数根;③若c是方程
也一定有两个不等的实数根;③若c是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;④若m是方程
成立;④若m是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立.其中正确地只有 ( )
成立.其中正确地只有 ( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A沿边AB向点B以1 cm/s的速度移动;同时点Q从点B沿边BC向点C以2 cm/s的速度移动,设运动时间为t s.问:
(1)几秒后△PBQ的面积等于8 cm2?
(2)是否存在t,使△PDQ的面积等于26 cm2?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com